Tổng hợp công thức tính xác suất thống kê và bài tập

Xác suất thống kê là gì ? Công thức tính xác suất thống kê như thế nào ? Đây là những câu hỏi luôn được rất nhiều người chăm sóc. Xác suất thống kê là môn học mà hầu hết những bạn học viên Đại Học đều được học. Hãy cùng Góc Yêu Bé khám phá khái niệm, công thức của xác suất thống kê nhé .

Xem thêm:

Khái niệm về xác suất thống kê

Xác suất là độ đo của sử dụng trong toán học để đo tính phi chắc như đinh của năng lực xảy ra một sự kiện .

Thống kê là một phần trong toán học của khoa học, nó gắn liền với tập hợp dữ liệu, phân tích, giải thích và thảo luận về một vấn đề nào đó.

Xác suất thống kê có ưu điểm lớn là không yên cầu những điều kiện kèm theo vận dụng như so với những định nghĩa cổ xưa, mà nó dựa vào những quan sát thực tế để làm cơ sở Tóm lại về xác suất xảy ra của một biến cố .

Tổng hợp công thức tính xác xuất thống kê

Công thức cộng xác suất

P(A + B) = P(A) + P(B) – P(AB)

Công thức xác suất có điều kiện

P(A/B) = P(AB)/P(B), P(B/A) = P(AB)/P(A)

Công thức nhân xác suất

P(AB) = P(A).P(B/A) = P(B).P(A/B)

Công thức Bernoulli

Lưu ý: Xác suất để biến cố A xảy ra trong mỗi phép thử và q = 1 – p.

Công thức tính xác suất thống kê đầy đủ nhất – Công thức Bayes

Hệ biến cố gồm n thành phần là A1, A2 … An có tên gọi là một phép phân hoạch của

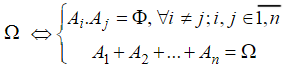
Công thức tính xác xuất thống kê rất đầy đủ là :

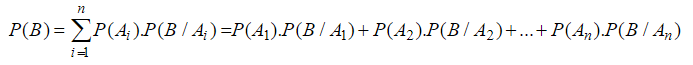
Công thức Bayes là :
P. ( Ai / B ) = [ P ( Ai ) P. ( B / Ai ) / P. ( B )
Với P. ( B ) = P ( A1 ). P ( B / A1 ) + P. ( A2 ). P ( B / A2 ) + … + P. ( An ). P ( B / An )

Bài tập tính xác suất thống kê có lời giải chi tiết

Bài tập 1: Một hộp bút có 100 cái bút giống nhau được ghi các số từ 1 đến 100, rút ngẫu nhiên hai bút rồi đặt theo thứ tự từ trái sang phải. Tính xác suất?

a. Rút được 2 bút nên một số có hai chữ số

b. Rút được 2 bút nên 1 số ít chia hết cho 5

Lời giải

a. Hai bút rút được nên một số ít hai chữ số
P. ( A ) = 9.8 / 100.99 ≈ 0,0073
b. hai bút rút được nên 1 số ít chia hết cho 5
Số chia hết cho 5 tận cùng phải bằng 0 hoặc 5. Do vậy, để có biến cố B thích hợp với ta rút cây bút thứ hai một cách tùy ý trong 20 bút mang những số 5, 10, 15, 20 … 95, 100 và rút 1 trong 99 cây bút còn lại đặt vào vị trí đầu. Bởi vậy số trường hợp thuận tiện cho là 99,20
P. ( B ) = 99.20 / A2100 = 0,20

Bài tập 2: Một hộp đựng kẹo có 5 chiếc kẹo còn hạn sử dụng và 3 chiếc kẹo hết hạn sử dụng. Chọn ngẫu nhiên lần lượt không trả lại 2 chiếc kẹo. Tính xác suất để:

a. cả 2 chiếc kẹo được chọn đều còn hạn sử dụng
b trong 2 chiếc kẹo có tối thiểu một chiếc kẹo còn hạn sử dụng

Lời giải

Chọn ngẫu nhiên lần lượt không trả lại 2 trong 12 chiếc kẹo nên các trường hợp đồng khả năng là

a. “ Cả 2 chiếc kẹo được chọn đều còn hạn sử dụng ”

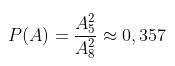
b. “ Trong hai chiếc kẹo được chọn có tối thiểu một chiếc kẹo còn hạn sử dụng ”

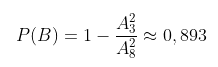
Hy vọng với những khái niệm, công thức và bài tập tính xác suất thống kê ở trên sẽ giúp bạn đọc nắm rõ về kỹ năng và kiến thức, vận dụng công thức tương thích và hoàn toàn có thể xử lý tổng thể những bài tập về xác suất thống kê. Nếu như vẫn có bài tập khó khăn vất vả không giải được hãy để lại phản hồi bên dưới nhé, chúng tôi sẽ cùng những bạn giải đáp vướng mắc đó trong thời hạn sớm nhất .

Source: https://evbn.org
Category: Góc Nhìn