Một số bài toán liên quan đến tích vô hướng của hai vectơ – https://leading10.vn

Phương pháp giải toán:
Bài toán 1: Tính tích vô hướng của các vectơ. Sử dụng các công thức:
• $\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos (\widehat {\overrightarrow a ,\overrightarrow b }).$
• Các tính chất của phép toán tích vô hướng của hai vectơ và các hằng đẳng thức về tích vô hướng như:
${\left( {\vec a \pm \vec b} \right)^2} = {\left| {\vec a} \right|^2} + {\left| {\vec b} \right|^2} \pm 2\vec a.\vec b.$
$(\vec a + \vec b).(\vec a – \vec b) = {\vec a^2} – {\vec b^2}.$
• $\overrightarrow a .\overrightarrow b = \overrightarrow a .\overrightarrow {b’} $, trong đó $\overrightarrow {b’} $ là hình chiếu của $\overrightarrow b $ lên giá của $\overrightarrow a .$

Bài toán 2: Chứng minh các đẳng thức về tích vô hướng. Sử dụng:
• Định nghĩa và tính chất của tích vô hướng phối hợp với các quy tắc về các phép toán vectơ.
• Công thức hình chiếu.
• Đối với các đẳng thức có liên quan đến độ dài thì chú ý: ${\overrightarrow {AB} ^2} = {\left| {\overrightarrow {AB} } \right|^2} = {(\overrightarrow {OB} – \overrightarrow {OA} )^2}.$

Ví dụ minh họa:
Ví dụ 1: Cho tam giác đều $ABC$ cạnh $a.$ Tính:
a) $\overrightarrow {AB} .\overrightarrow {AC} $, $\overrightarrow {AB} .\overrightarrow {BC} $, $\overrightarrow {BC} .\overrightarrow {CA} .$
b) $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} .$

a) Ta có: $\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos (\widehat {\overrightarrow {AB} ;\overrightarrow {AC} })$ $ = AB.AC.\cos \widehat {BAC}$ $ = a.a.\cos {60^0} = \frac{{{a^2}}}{2}.$
Dựng $\overrightarrow {AD} = \overrightarrow {BC} $, ta có: $\overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {AB} .\overrightarrow {AD} $ $ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos (\widehat {\overrightarrow {AB} ;\overrightarrow {AD} })$ $ = AB.AD.\cos {120^0}$ $ = a.a.\cos {120^0} = – \frac{{{a^2}}}{2}.$
Ta có thể tính tương tự như trên hoặc sử dụng quy tắc $3$ điểm: $\overrightarrow {BC} .\overrightarrow {CA} = (\overrightarrow {AC} – \overrightarrow {AB} ).( – \overrightarrow {AC} )$  $ = – {\overrightarrow {AC} ^2} + \overrightarrow {AB} .\overrightarrow {AC} $ $ = – {a^2} + \frac{{{a^2}}}{2} = – \frac{{{a^2}}}{2}.$
b) Áp dụng kết quả trên, ta có: $\overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {BC} .\overrightarrow {CA} = \overrightarrow {CA} .\overrightarrow {AB} = – \frac{{{a^2}}}{2}.$
Suy ra: $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} $ $ = 3\left( { – \frac{{{a^2}}}{2}} \right) = – \frac{{3{a^2}}}{2}.$
Cách khác: Ta có thể tính trực tiếp không dựa vào kết quả câu a.
Ta có: $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 .$
Suy ra: ${\left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right)^2} = 0.$
Do đó: ${\overrightarrow {AB} ^2} + {\overrightarrow {BC} ^2} + {\overrightarrow {CA} ^2}$ $+2\left( {\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} } \right) = 0.$
Vậy $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} $ $ = – \frac{{A{B^2} + B{C^2} + C{A^2}}}{2} = – \frac{{3{a^2}}}{2}.$

Ví dụ 2: Cho tam giác $ABC$ với $AB = 5 cm$, $BC = 7cm$, $CA = 8cm.$
a) Tính $\overrightarrow {AB} .\overrightarrow {AC} .$ Suy ra số đo của góc $\widehat A.$
b) Tính $\overrightarrow {CA} .\overrightarrow {CB} $, từ đó suy ra $\overrightarrow {CB} .\overrightarrow {CD} $ với $D$ là điểm nằm trên cạnh $CA$ sao cho $CD = 4 cm.$

a) Ta có: $\overrightarrow {BC} = \overrightarrow {AC} – \overrightarrow {AB} .$
Suy ra: ${\overrightarrow {BC} ^2} = {\overrightarrow {AC} ^2} + {\overrightarrow {AB} ^2} – 2\overrightarrow {AC} .\overrightarrow {AB} .$
Vậy: $\overrightarrow {AC} .\overrightarrow {AB} = \frac{{A{C^2} + A{B^2} – B{C^2}}}{2}$ $ = \frac{{64 + 25 – 49}}{2} = 20.$
Mặc khác: $\overrightarrow {AC} .\overrightarrow {AB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AB} } \right|\cos \left( {\widehat {\overrightarrow {AC} .\overrightarrow {AB} }} \right)$ $ = AC.AB.\cos A.$
Suy ra: $\cos A = \frac{{\overrightarrow {AC} .\overrightarrow {AB} }}{{AC.AB}} = \frac{{20}}{{8.5}} = \frac{1}{2}.$
Do đó: $\widehat A = {60^0 }.$
b) Tương tự ở trên ta có:
$\overrightarrow {CA} .\overrightarrow {CB} = \frac{{C{A^2} + C{B^2} – A{B^2}}}{2}$ $ = \frac{{64 + 49 – 25}}{2} = 44.$
Suy ra: $\cos \left( {\widehat {\overrightarrow {CA} ,\overrightarrow {CB} }} \right) = \frac{{\overrightarrow {CA} .\overrightarrow {CB} }}{{\left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|}}$ $ = \frac{{44}}{{8.7}} = \frac{{11}}{{14}}.$
Mà $D$ nằm trên cạnh $CA$ nên $(\overrightarrow {CD} ,\overrightarrow {CB} ) = (\overrightarrow {CA} ,\overrightarrow {CB} ).$
Do vậy $\overrightarrow {CD} .\overrightarrow {CB} = \left| {\overrightarrow {CD} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\widehat {\overrightarrow {CA} .\overrightarrow {CB} }} \right)$ $ = 4.7 \cdot \frac{{11}}{{14}} = 22.$

Ví dụ 3: Cho hình vuông $ABCD$ cạnh $a$, tâm $O$. $M$ là điểm tùy ý trên đường tròn nội tiếp hình vuông và $N$ là điểm tùy ý trên cạnh $BC$. Tính:
a) $\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} .$
b) $\overrightarrow {NA} .\overrightarrow {AB} $ và $\overrightarrow {NO} .\overrightarrow {BA} .$

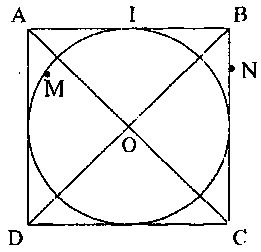
a) Ta có: $\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} $ $ = (\overrightarrow {MO} + \overrightarrow {OA} )(\overrightarrow {MO} + \overrightarrow {OB} )$ $ + (\overrightarrow {MO} + \overrightarrow {OC} )(\overrightarrow {MO} + \overrightarrow {OD} )$ $ = {\overrightarrow {MO} ^2} + \overrightarrow {MO} .\overrightarrow {OA} $ $ + \overrightarrow {MO} .\overrightarrow {OB} + \overrightarrow {OA} .\overrightarrow {OB} $ $ + {\overrightarrow {MO} ^2} + \overrightarrow {MO} .\overrightarrow {OD} $ $ + \overrightarrow {MO} .\overrightarrow {OC} + \overrightarrow {OC} .\overrightarrow {OD} $ $ = 2M{O^2} + \overrightarrow {MO} (\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} )$ $ + \overrightarrow {OA} .\overrightarrow {OB} + \overrightarrow {OC} .\overrightarrow {OD} $ $ = 2M{O^2} = \frac{{{a^2}}}{2}$ (vì $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \vec 0$ và $OA \bot OB$, $OC \bot OD$ nên $\overrightarrow {OA} .\overrightarrow {OB} = \overrightarrow {OC} .\overrightarrow {OD} = 0$).
b) Ta có:
$\overrightarrow {NA} .\overrightarrow {AB} = \overrightarrow {BA} .\overrightarrow {AB} $ $ = – \overrightarrow {AB} .\overrightarrow {AB} = – A{B^2} = – {a^2}.$
$\overrightarrow {NO} .\overrightarrow {BA} = \overrightarrow {BI} .\overrightarrow {BA} $ $ = \frac{1}{2}a.a = \frac{{{a^2}}}{2}$ (với $I$ là trung điểm của $AB$).

Ví dụ 4: Cho $4$ điểm $A$, $B$, $C$, $D$ bất kỳ. Chứng minh rằng:
a) $\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0$ (hệ thức Euler). Suy ra $3$ đường cao của một tam giác thì đồng quy.
b) $A{D^2} + B{C^2} – A{C^2} – B{D^2}$ $ = 2\overrightarrow {AB} .\overrightarrow {CD} .$

a) Ta có: $\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} $ $ = \overrightarrow {AB} (\overrightarrow {AD} – \overrightarrow {AC} )$ $ + \overrightarrow {AC} (\overrightarrow {AB} – \overrightarrow {AD} )$ $ + \overrightarrow {AD} (\overrightarrow {AC} – \overrightarrow {AB} )$ $ = \overrightarrow {AB} .\overrightarrow {AD} – \overrightarrow {AB} .\overrightarrow {AC} $ $ + \overrightarrow {AC} .\overrightarrow {AB} – \overrightarrow {AC} .\overrightarrow {AD} $ $ + \overrightarrow {AD} .\overrightarrow {AC} – \overrightarrow {AD} .\overrightarrow {AB} = 0.$
Gọi $H$ là giao điểm của $2$ đường cao xuất phát từ $B$ và $C$ của tam giác $ABC.$ Khi đó áp dụng hệ thức Euler đối với $4$ điểm $H$, $A$, $B$, $C$ ta có: $\overrightarrow {HA} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {CA} + \overrightarrow {HC} .\overrightarrow {BA} = 0.$
Ta có $HB \bot CA$, $HC \bot BA$ nên $\overrightarrow {HB} .\overrightarrow {CA} = \overrightarrow {HC} .\overrightarrow {BA} = 0.$
Suy ra: $\overrightarrow {HA} .\overrightarrow {BC} = 0.$
Do đó $HA \bot BC$ hay $HA$ là đường cao của tam giác $ABC.$
Vậy $3$ đường cao tam giác $ABC$ đồng quy tại một điểm.
b) Ta có: $A{D^2} + B{C^2} – A{C^2} – B{D^2}$ $ = {\overrightarrow {AD} ^2} – {\overrightarrow {AC} ^2} + {\overrightarrow {BC} ^2} – {\overrightarrow {BD} ^2}$ $ = (\overrightarrow {AD} + \overrightarrow {AC} )(\overrightarrow {AD} – \overrightarrow {AC} )$ $ + (\overrightarrow {BC} + \overrightarrow {BD} )(\overrightarrow {BC} – \overrightarrow {BD} )$ $ = (\overrightarrow {AD} + \overrightarrow {AC} ).\overrightarrow {CD} $ $ + (\overrightarrow {BC} + \overrightarrow {BD} ).\overrightarrow {DC} $ $ = (\overrightarrow {AD} + \overrightarrow {AC} – \overrightarrow {BC} – \overrightarrow {BD} ).\overrightarrow {CD} $ $ = (\overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {AC} + \overrightarrow {CB} ).\overrightarrow {CD} $ $ = (\overrightarrow {AB} + \overrightarrow {AB} ).\overrightarrow {CD} $ $ = 2\overrightarrow {AB} .\overrightarrow {CD} .$

Ví dụ 5: Cho tam giác $ABC$ có $AM$, $AH$ lần lượt là trung tuyến và đường cao của tam giác ứng với cạnh $BC.$ Chứng minh rằng:
a) $\overrightarrow {AB} .\overrightarrow {AC} = A{M^2} – \frac{{B{C^2}}}{4}.$
b) $A{B^2} + A{C^2} = 2A{M^2} + \frac{{B{C^2}}}{2}.$
c) $A{B^2} – A{C^2} = 2\overrightarrow {BC} .\overrightarrow {MH} .$

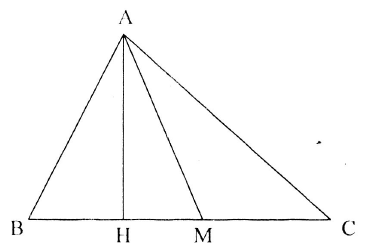
a) Ta có: $\overrightarrow {AB} .\overrightarrow {AC} $ $ = (\overrightarrow {AM} + \overrightarrow {MB} )(\overrightarrow {AM} + \overrightarrow {MC} )$ $ = (\overrightarrow {AM} + \overrightarrow {MB} )(\overrightarrow {AM} – \overrightarrow {MB} )$ $ = {\overrightarrow {AM} ^2} – {\overrightarrow {MB} ^2}$ $ = A{M^2} – \frac{{B{C^2}}}{4}.$
b) Ta có: $A{B^2} + A{C^2}$ $ = {\overrightarrow {AB} ^2} + {\overrightarrow {AC} ^2}$ $ = {(\overrightarrow {AM} + \overrightarrow {MB} )^2} + {(\overrightarrow {AM} + \overrightarrow {MC} )^2}$ $ = {(\overrightarrow {AM} + \overrightarrow {MB} )^2} + {(\overrightarrow {AM} – \overrightarrow {MB} )^2}$ $ = 2{\overrightarrow {AM} ^2} + 2{\overrightarrow {MB} ^2}$ $ = 2A{M^2} + 2M{B^2}$ $ = 2A{M^2} + \frac{{B{C^2}}}{2}.$
c) $A{B^2} – A{C^2}$ $ = {\overrightarrow {AB} ^2} – {\overrightarrow {AC} ^2}$ $ = (\overrightarrow {AB} – \overrightarrow {AC} )(\overrightarrow {AB} + \overrightarrow {AC} )$ $ = \overrightarrow {CB} .2\overrightarrow {AM} $ $ = 2\overrightarrow {CB} .\overrightarrow {HM} $ $ = 2\overrightarrow {BC} .\overrightarrow {MH} .$

Source: https://evbn.org
Category: Góc Nhìn