Trực tâm là gì? Tính chất và cách xác định trực tâm của tam giác
Mục Lục
Định nghĩa trực tâm là gì ?
Trực tâm hay trực tâm tam giác là gì? Trong một tam giác bất kì có ba đường cao. Ba đường này cùng đi qua một điểm, thì điểm này chính là trực tâm của tam giác.
Đường cao của tam giác là gì ? Đường cao của một tam giác chính là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối lập. Cạnh đối lập này thường được gọi là đáy tương ứng với mỗi đường cao .
Giả sử cho tam giác LMN có ba đường cao lần lượt là LP, MQ, NI. Gọi S là là giao điểm của ba đường cao trên thì S là trực tâm của tam giác LMN.
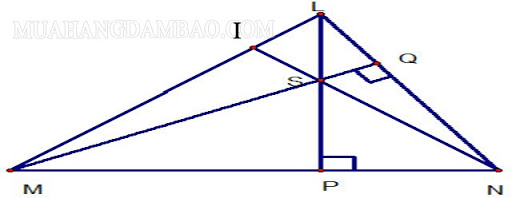
Cách xác lập trực tâm của một tam giác .
Trực tâm của tam giác là điểm giao nhau của ba đường cao trong tam giác. Tuy nhiên để xác lập trực tâm trong tam giác tất cả chúng ta không nhất thiết phải vẽ ba đường cao. Khi vẽ hai đường cao của tam giác ta đã hoàn toàn có thể xác lập được trực tâm của tam giác rồi. Đối với những loại tam giác thường thì như tam giác nhọn tam giác tù hay tam giác cân tam giác đều thì ta đều có cách xác lập trực tâm giống nhau. Từ hai đỉnh của tam giác ta kẻ hai đường cao của tam giác đến hai cạnh đối lập. Hai cạnh đó giao nhau tại điểm nào thì điểm đó chính là trực tâm của tam giác. Và đường cao còn lại chắc như đinh cũng đi qua trực tâm của tam giác dù ta không cần kẻ .
Tuy nhiên so với tam giác vuông thì việc xác lập đường cao có khác một chút ít. Tam giác vuông có hai cạnh góc vuông chính là hai đường cao của tam giác vì hai cạnh vuông góc với nhau. Chính vì thế trực tâm của tam giác vuông trùng với đỉnh của góc vuông .

Xem thêm: Triết học – Wikipedia tiếng Việt
Những đặc thù của trực tâm trong tam giác .
- Tính chất 1: Trong một tam giác cân thì đường trung trực tương ứng với cạnh đáy sẽ đồng thời là đường phân giác, đường cao và đường trung tuyến của tam giác đó.
- Tính chất 2: Trong một tam giác, nếu như một đường trung tuyến đồng thời là đường phân giác thì tam giác đó sẽ là tam giác cân.
- Tính chất 3: Trong một tam giác, nếu như một đường trung tuyến đồng thời là đường trung trực thì tam giác đó sẽ là tam giác cân.
- Tính chất 4: Trực tâm của tam giác nhọn ABC sẽ trùng với tâm của đường tròn nội tiếp tam giác có ba đỉnh là chân của ba đường cao từ các đỉnh A, B, C đến các cạnh đối diện BC, AC, AB tương ứng.
- Tính chất 5: Đường cao tam giác ứng với một đỉnh cắt đường tròn ngoại tiếp tại một điểm thứ hai sẽ là đối xứng của trực tâm qua cạnh tương ứng.
Từ những đặc thù trên ta rút ra hệ quả như sau : Trong một tam giác đều, trực tâm, trọng tâm, điểm nằm trong tam giác, điểm cách đều ba đỉnh, và cách đều ba cạnh là bốn điểm này đều trùng nhau, là một điểm .
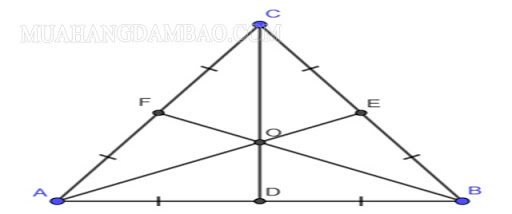
Bài tập vận dụng .
Trực tâm của tam giác Open rất nhiều trong hình học khoảng trống như tìm trực tâm trong khoảng trống. Chúng ta có bài tập sau .
Tìm tọa độ trực tâm H biết tam giác ABC tọa độ có A ( – 2 ; 6 ), B ( – 2 ; 9 ) ; C ( 9 ; 8 ). Hãy tìm trực tâm của tam giác trong khoảng trống xyz .
Lời giải:
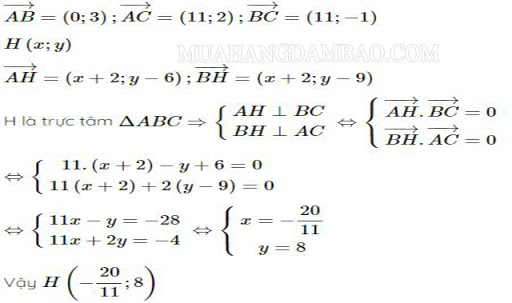
Bài viết trên là tổng hợp những kỹ năng và kiến thức tương quan đến trực tâm, kỳ vọng qua những san sẻ trên bạn đã nắm được kiến thức và kỹ năng trực tâm là gì ? Định nghĩa, đặc thù và cách xác lập trực tâm của tam giác đúng chuẩn nhất, bổ trợ cho bạn những thông tin hữu dụng cho quy trình học tập và nghiên cứu và điều tra của bạn, chúc bạn thành công xuất sắc .
Source: https://evbn.org
Category: Làm Gì















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


