Khái niệm hai tam giác đồng dạng – Các trường hợp đồng dạng toán 8

5/5 – ( 6 votes )

Trong toán học và đặc biệt là ở phần hình học, hình đồng dạng và đặc biệt 2 tam giác đồng dạng đều là những kiến thức rất quan trọng mà học sinh cần phải nắm rõ. Để tìm hiểu rõ hơn về khái niệm hai tam giác đồng dạng và ba trường hợp đồng dạng, hãy tham khảo ngay bài viết sau đây của Toppy các bạn nhé.

Khái niệm hai tam giác đồng dạng

Trong đời sống, những bạn hoàn toàn có thể sẽ đôi lúc phát hiện những hình ảnh có hình dạng giống hệt nhau nhưng lại có size khác nhau, những hình ảnh này còn được gọi là hình đồng dạng .

Thế nào là 2 tam giác đồng dạng?

Khi cho 2 tam giác ABC và tam giác A’B’C’, ta xét các cặp góc và tính tỷ số 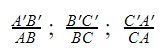2 tam giác ABC và A’B’C’ sẽ được xem là đồng dạng nếu góc A = góc A’, góc B = góc B’, góc C = góc C’ và .

Như vậy, 2 tam giác sẽ được xem là đồng dạng với nhau nếu 2 tam giác đó có những góc tương ứng bằng nhau và những cạnh có tỷ suất tương ứng với nhau .

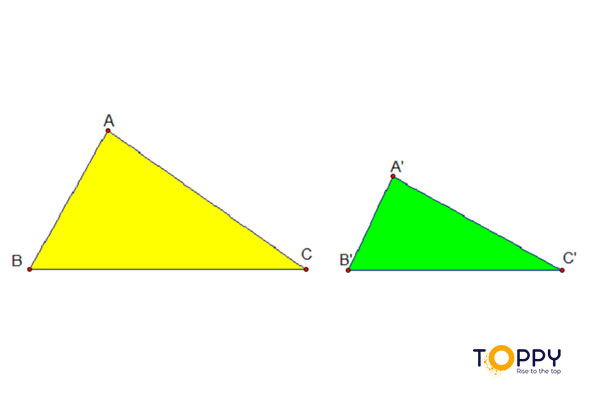
Ký hiệu của 2 tam giác đồng dạng

Cho 2 tam giác ABC và A’B’C’, 2 tam giác đồng dạng với nhau sẽ có ký hiệu là:

△ ABC ∼ △ A’B ’ C ’
Khi những cạnh có tỷ số tương ứng là k = thì k sẽ được gọi là tỷ số đồng dạng .

Tính chất của 2 tam giác đồng dạng

Theo như khái niệm hai tam giác đồng dạng, chúng ta có thể suy ra được 3 tính chất cơ bản sau đây:

• Mỗi tam giác đồng dạng với chính bản thân nó .
• Nếu △ ABC ∼ △ A’B ’ C ’ thì △ A’B ’ C ’ ∼ △ ABC .
• Nếu 2 tam giác đều cùng đồng dạng với một tam giác khác thì 2 tam giác đó sẽ đồng dạng với nhau. Ký hiệu : Nếu △ A’B ’ C ’ ∼ △ A ” B ” C ” và △ A ” B ” C ” ∼ △ ABC thì △ ABC ∼ △ A’B ’ C ’ .

Đặc biệt, ngoài 3 tính chất trên, các bạn cũng cần phải lưu ý rằng hai tam giác bằng nhau thì đồng dạng nhưng hai tam giác đồng dạng sẽ không có nghĩa là sẽ bằng nhau.

Định lý liên quan đến hai tam giác đồng dạng

Tiếp theo khái niệm hai tam giác đồng dạng và tính chất của tam giác đồng dạng, Toppy sẽ chia sẻ định lý liên quan đến 2 tam giác đồng dạng.

Định lý được phát biểu như sau : Nếu có 1 đường thẳng song song với 2 cạnh của một tam giác và đồng thời cắt cạnh còn lại của tam giác đó thì sẽ tạo thành một tam giác mới, tam giác đó sẽ đồng dạng với tam giác đã được cho trước .

Nói cách khác, với △ABC đã cho trước, điểm D ∈ AB và điểm E ∈ AC, ta sẽ có △ABC ∼ △ADE. Đặc biệt, định lý này cũng có thể áp dụng được với trường hợp có một đường thẳng d cắt đoạn kéo dài của 2 đoạn thẳng trong tam giác và đồng thời song song với đoạn còn lại.

Những trường hợp đồng dạng của tam giác

Bên cạnh khái niệm hai tam giác đồng dạng, những trường hợp đồng dạng của hai tam giác cũng vô cùng quan trọng. Hãy cùng Toppy phân tích những trường hợp của 2 tam giác đồng dạng nhé.

Trường hợp 1: Trường hợp Góc – Góc

Trường hợp đồng dạng thứ nhất của hai tam giác đồng dạng là trường hợp Góc – Góc. Theo đó, trường hợp này được phát biểu như sau: Hai tam giác mà có hai cặp góc bằng nhau chính là hai tam giác đồng dạng với nhau.

Khi cho 2 △ ABC và △ A’B ’ C ’, nếu có góc A = góc A ’ và góc B = góc B ’ thì △ ABC ∼ △ A’B ’ C ’ .

Trường hợp 2: Trường hợp Cạnh – Cạnh – Cạnh

Trường hợp đồng dạng thứ hai của hai tam giác đồng dạng là trường hợp Cạnh – Cạnh – Cạnh. Trường hợp này được phát biểu như sau: Nếu 2 tam giác đã cho trước có 3 cặp cạnh tỉ lệ với nhau thì 2 tam giác đó đồng dạng với nhau.

Khi cho △ABC và △A’B’C’, nếu thì △ABC ∼ △A’B’C’.

Trường hợp 3: Trường hợp Cạnh – Góc – Cạnh

Trường hợp đồng dạng thứ ba của hai tam giác đồng dạng là trường hợp Cạnh – Góc – Cạnh. Trường hợp này được phát biểu như sau: Nếu 2 tam giác đã cho trước có hai cặp cạnh tương ứng tỉ lệ với nhau và 2 góc xen giữa bằng nhau thì 2 tam giác này đồng dạng với nhau.

Khi cho △ABC và △A’B’C’, nếu ‘và góc B = góc B’ thì △ABC ∼ △A’B’C’.

Trường hợp đồng dạng của 2 tam giác vuông

Ngoài 3 trường hợp đồng dạng trên, những bạn cần phải nắm vững 2 trường hợp khác, gồm có :

• Trong 2 tam giác vuông, nếu có một cặp góc nhọn bằng nhau thì 2 tam giác đó đồng dạng với nhau .
• Trong 2 tam giác vuông, nếu sống sót 2 cặp cạnh tỉ lệ tương ứng với nhau thì 2 tam giác đó đồng dạng với nhau .

Như vậy, bài viết trên đã cung cấp cho các bạn đọc khái niệm hai tam giác đồng dạng và các tính chất tương ứng. Ngoài ra, việc nắm rõ những trường hợp đồng dạng sẽ giúp các bạn giải bài tập dễ dàng hơn. Để tìm hiểu thêm nhiều kiến thức hữu ích khác, hãy truy cập ngay vào trang web https://evbn.org/ nhé.

Tìm hiểu thêm: 

Giải pháp toàn diện giúp con đạt điểm 9-10 dễ dàng cùng Toppy

Với tiềm năng lấy học viên làm TT, Toppy chú trọng việc kiến thiết xây dựng cho học viên một lộ trình học tập cá thể, giúp học viên nắm vững cơ bản và tiếp cận kiến thức và kỹ năng nâng cao nhờ mạng lưới hệ thống nhắc học, thư viện bài tập và đề thi chuẩn khung năng lượng từ 9 lên 10 .

Kho học liệu khổng lồ

Kho video bài giảng, nội dung minh hoạ sinh động, dễ hiểu, kết nối học viên vào hoạt động giải trí tự học. Thư viên bài tập, đề thi nhiều mẫu mã, bài tập tự luyện phân cấp nhiều trình độ. Tự luyện – tự chữa bài giúp tăng hiệu suất cao và rút ngắn thời hạn học. Kết hợp phòng thi ảo ( Mock Test ) có giám thị thật để chuẩn bị sẵn sàng sẵn sàng chuẩn bị và tháo gỡ nỗi lo về bài thi IELTS .

Nền tảng học tập thông minh, không giới hạn, cam kết hiệu quả

Chỉ cần điện thoại cảm ứng hoặc máy tính / máy tính là bạn hoàn toàn có thể học bất kỳ khi nào, bất kể nơi đâu. 100 % học viên thưởng thức tự học cùng TOPPY đều đạt hiệu quả như mong ước. Các kiến thức và kỹ năng cần tập trung chuyên sâu đều được cải tổ đạt hiệu suất cao cao. Học lại không tính tiền tới khi đạt !

Tự động thiết lập lộ trình học tập tối ưu nhất

Lộ trình học tập cá nhân hóa cho mỗi học viên dựa trên bài kiểm tra đầu vào, hành vi học tập, kết quả luyện tập (tốc độ, điểm số) trên từng đơn vị kiến thức; từ đó tập trung vào các kỹ năng còn yếu và những phần kiến thức học viên chưa nắm vững.

Trợ lý ảo và Cố vấn học tập Online đồng hành hỗ trợ xuyên suốt quá trình học tập

Kết hợp với ứng dụng AI nhắc học, nhìn nhận học tập mưu trí, chi tiết cụ thể và đội ngũ tương hỗ vướng mắc 24/7, giúp kèm cặp và động viên học viên trong suốt quy trình học, tạo sự yên tâm phó thác cho cha mẹ .

Source: https://evbn.org
Category : Làm Gì