Tập hợp là gì? Các phép toán tập hợp và biểu đồ ven

Tập hợp, biểu đồ ven là những khái niệm quen thuộc chúng ta đã học ngay từ bài đầu tiên, khi ta làm quen với các tập hợp số tự nhiên,  số vô tỉ, số thực, số nguyên, số hữu tỉ trong chương trình toán THCS. Bài viết sau đây thapgiainhietliangchi xin giới thiệu đến các bạn lý thuyết tập hợp là gì? Các phép toán tập hợp, bài tập về tập hợp để vận dụng.

Lý thuyết tập hợp

Khái niệm tập hợp là gì? 

Tập hợp là một khái niệm cơ bản (không thể định nghĩa) của toán học. Các tập hợp thường sẽ được kí hiệu bằng những chữ cái in hoa như A, B, …,N, X, Y. Hoặc các phần tử của tập hợp cũng được kí hiệu bằng các chữ in thường như a, b,…, n, x, y.

Phần tử của tập hợp là gì? Kí hiệu a ∈ A dùng để chỉ a là một phần tử của tập hợp A hay a thuộc tập hợp A. Ngược lại a∉ A để chỉ a không thuộc A, a không phải là phần tử của tập hợp A.

Một tập hợp có thể được thể hiện bằng cách liệt kê các phần tử của nó hoặc được chỉ ra bằng cách nêu tính chất đặc trưng của các phân tử của tập hợp.

Ví dụ về tập hợp như: A = {1, 2} hay A = { x ∊ R/ x² – 3x +2 = 0 }

Và một tập hợp mà không có phân tử nào sẽ được gọi là tập hợp rỗng, kí hiệu Ø. 

— Tập hợp của các số tự nhiên đã được quy ước kí hiệu là N

N={0, 1, 2, 3, 4, 5, 6 ..}

— Tập hợp của các số nguyên đã được quy ước kí hiệu là Z

Z={…-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 …}

Tập hợp số nguyên sẽ bao gồm các phân tử là các số tự nhiên và các phần tử là số đối của các số tự nhiên.

Tập hợp của các số nguyên dương đã được kí hiệu là N*

— Tập hợp của các số hữu tỉ, đã được quy ước kí hiệu là Q

Q={ a/b; a, b∈Z, b≠0}

Một số hữu tỉ cũng có thể được biểu diễn bằng một số thập phân hữu hạn hoặc một số thập phân vô hạn tuần hoàn.

— Tập hợp của các số thực đã được quy ước kí hiệu là R

Mỗi số sẽ được biểu diễn bằng một số thập phân vô hạn không tuần hoàn hay còn được ta gọi là một số vô tỉ. Tập hợp các số vô tỉ đã được quy ước kí hiệu là I. Tập hợp của các số thực sẽ bao gồm các số hữu tỉ và các số vô tỉ.

— Các tập hợp con thường gặp nhất của tập hợp số thực

Kí hiệu –∞ được đọc là âm vô cực (hoặc âm vô cùng), kí hiệu +∞ được đọc là dương vô cực (hoặc dương vô cùng)

— Mối quan hệ các tập hợp số

Ta có được: R = Q ∪ I

Tập N ; Z ; Q ; R.

Khi đó quan hệ bao hàm giữa các tập hợp số sẽ là như sau : N ⊂ Z ⊂ Q ⊂ R

Mối quan hệ giữa các tập hợp số còn được thể hiện trực quan qua biểu đồ Ven.

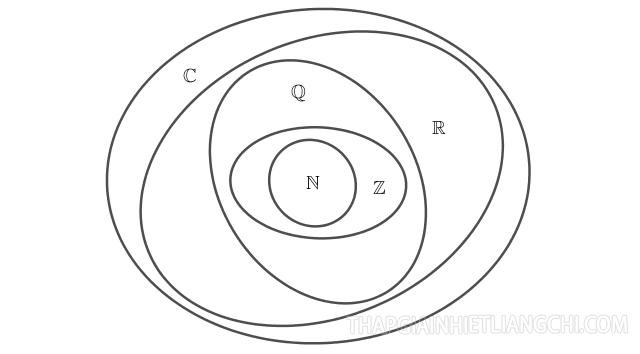
Biểu đồ Ven

Để minh họa một tập hợp người ta thường dùng một đường cong khép kín giới hạn trên một phần mặt phẳng. Các điểm thuộc phần mặt phẳng này được dùng để chỉ các phần tử của tập hợp ấy.

Tập hợp con

tập hợp con là gì? Ta gọi A là tập hợp con của B, được kí hiệu là 

A ⊂ B ⇔ x ∈ A => x ∈ B

Hai tập hợp bằng nhau

Hai tập hợp A và B được gọi là hai tập hợp bằng nhau và kí hiệu là A = B, nếu tất cả các phần tử của chúng đều như nhau 

A = B ⇔ A ⊂ B và B ⊂ A.

Các phép toán về tập hợp

Để có thể làm được các bài tập về tập hợp chúng ta phải nắm chắc các phép toán về tập hợp.

Bài tập về tập hợp để vận dụng

Bài tập 1: Hãy chọn câu trả lời đúng nhất trong các câu sau đây:

1. [a;b] ⊂ (a;b]

2. [a;b) ⊂ (a;b]

3. [a;b] ⊂ (a;b)

4. (a;b], [a;b) đều là các tập con của [a;b]

Giải: Chọn đáp án đúng là 4, vì [a;b] là tập lớn nhất trong 4 tập hợp 

Bài tập 2:  Bạn hãy xác định mỗi tập hợp sau đây: 

1. [-2;4)∪(0;5]

2. (-1;6]∩[1;7)

3. (-∞;7)\(1;9)

Giải:

1. [-2;4)∪(0;5]=[-2;5]

2. (-1;6]∩[1;7)=[1;6]

3. (-∞;7)\(1;9)=(-∞;1]

Đây là dạng toán thường xuyên gặp nhất, để giải nhanh dạng toán này chúng ta cần vẽ các tập hợp lên trục số thực trước, phần lấy ta sẽ giữa nguyên còn phần không lấy ta sẽ gạch bỏ đi để dễ phân biệt. Sau đó việc lấy giao, hợp hay hiệu sẽ nhanh chóng, dễ dàng hơn.

Bài tập 3: Bạn hãy xác định mỗi tập hợp sau

1. (-∞;1]∩(1;2)

2. (-5;7]∩[3;8)

3. (-5;2)∪[-1;4]

4. (-3;2)\[0;3]

5. R\(-∞;9)

Giải:

1. (-∞;1]∩(1;2) ≠ ∅

2. (-5;7]∩[3;8) = [3;7)

3. (-5;2)∪[-1;4] = (-1;2)

4. (-3;2)\[0;3] = (-3;0]

5. R\(-∞;9) = [9;+∞)

Bài tập 4: Hãy xác định các tập hợp sau đây và biểu diễn chúng trên trục số

1. [-3;1) ∪ (0;4]

2. [-3;1) ∩ (0;4]

3. (-∞;1) ∪ (2;+∞)

4. (-∞;1) ∩ (2;+∞)

Bài tập 5:  A=(-2;3) cùng  B=[1;5]. Xác định các tập hợp sau đây A ∪ B, A ∩ B, A\B, B\A.

Bài tập 6: Cho tập hợp A={x € R||x ≤ 4}; B={x€ R|-2 ≤ x+1 < 3}. Hãy viết các tập sau đây dưới dạng khoảng – đoạn – nửa khoảng: A ∩ B, A\B, B\A, R\(A∪B)

Bài tập 7: Cho tập hợp  A={x € R|-3 ≤ x ≤ 5} và B = {x € Z|-1< x ≤ 5}

Hãy xác định các tập hợp sau đây: A ∪ B, A ∩ B, A\B, B\A

Bài tập 8: Cho tập hợp A={x € R|x>2} và B={x € R|-1 < x ≤ 5}

Hãy cùng xác định các tập hợp sau đây: A ∪ B, A ∩ B, A\B, B\A

Bài tập 9: Cho tập hợp A={2,7} và B=(-3,5]. Hãy cùng xác định các tập hợp sau đây : A ∪ B, A ∩ B, A\B, B\A

Bài tập 10: Hãy xác định các tập hợp sau đây và biểu diễn lại chúng trên trục số

1. R\((0;1) ∪ (2;3))

2. R\((3;5) ∩ (4;6)

3. (-2;7)\[1;3]

4. ((-1;2) ∪ (3;5))\(1;4)

Bài viết trên là lý thuyết tập hợp, hy vọng qua bài viết các bạn đã nắm được tập hợp là gì? Nắm được biểu đồ ven, tập hợp con, phần tử của tập hợp đặc biệt là các phép toán tập hợp để có thể vận dụng giải quyết được các dạng bài tập.