Tam giác đồng dạng: Khái niệm, tính chất và cách chứng minh

Trong toán học, chắc hẳn các bạn đã từng nghe đến khái niệm tam giác đồng dạng. Vậy cụ thể thì tam giác đồng dạng là gì? Nó có những tính chất như thế nào? Các trường hợp đồng dạng của tam giác là những trường hợp nào? Trong bài viết này, chúng ta sẽ lần lượt giải đáp những thắc mắc trên. Hãy cùng chúng mình tìm hiểu rõ hơn nhé!

Khái niệm tam giác đồng dạng

Tam giác đồng dạng được định nghĩa như sau: Nếu một đường thẳng cắt hai cạnh của một tam giác bất kỳ và song song với cạnh còn lại thì nó sẽ tạo thành một tam giác mới đồng dạng với tam giác ban đầu.

Cụ thể là tam giác A’B’C’ được gọi là đồng dạng với tam giác ABC nếu đáp ứng được các điều kiện dưới đây:

• Góc A’ = góc A, góc B’ = góc B, góc C’ = góc C
• Tỉ lệ các cạnh là: A’B/AB = B’C’/BC = A’C’/AC

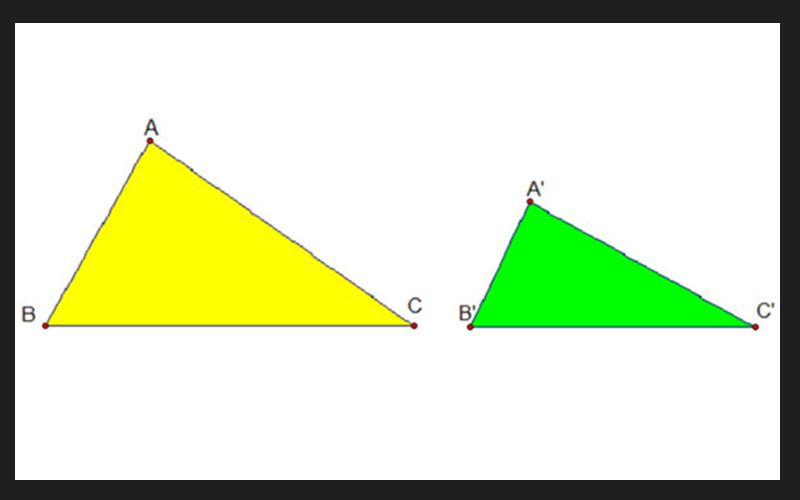
Kí hiệu tam giác đồng dạng

Ký hiệu đồng dạng được quy ước là ∼ ngược. Nếu tam giác ABC đồng dạng với tam giác A’B’C’ thì ta có ký hiệu: △ABC ∼ △A’B’C’.

Gọi tỉ lệ A’B/AB = B’C’/BC = A’C’/AC = k. Lúc này, k được gọi là tỉ số đồng dạng.

Tính chất tam giác đồng dạng

Xét về tính chất của tam giác đồng dạng, ta có những tính chất như sau:

• Mỗi tam giác đều đồng dạng với chính tam giác đó
• Nếu △ABC ∼ △A’B’C’ thì ngược lại, △A’B’C’ ∼ △ABC
• Trong trường hợp 2 tam giác đều cùng đồng dạng với một tam giác bất kỳ thì 2 tam giác đều này cũng sẽ đồng dạng với nhau. Ví dụ: △ABC ∼ △A’B’C’, mặt khác △A”B”C” ∼ △A’B’C’ thì suy ra △ABC ∼ △A”B”C”
• Ngoài ra, nếu hai tam giác bất kỳ bằng nhau thì sẽ đồng dạng với nhau. Nhưng hai tam giác đồng dạng với nhau thì không phải lúc nào cũng sẽ bằng nhau

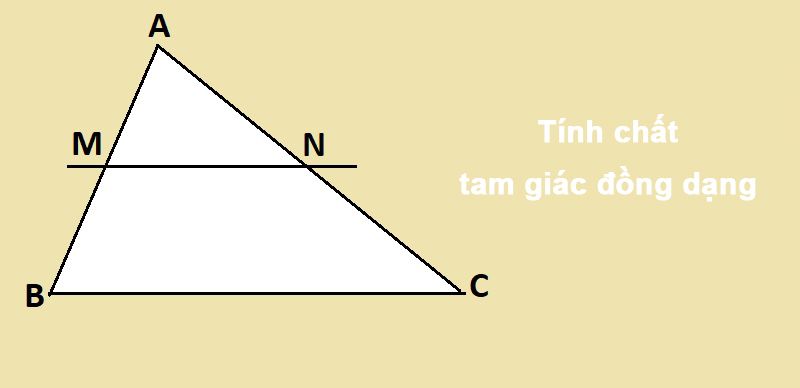
Các trường hợp đồng dạng của tam giác

Sau đây là các trường hợp đồng dạng của tam giác mà bạn cần phải nắm vững.

Tính chất đường phân giác

Tính chất đường phân giác của một tam giác được quy định như sau:

Trong một tam giác thì đường phân giác của một góc bất kỳ sẽ chia cạnh đối diện thành hai đoạn thẳng có tỉ lệ với hai cạnh kề của hai đoạn ấy.

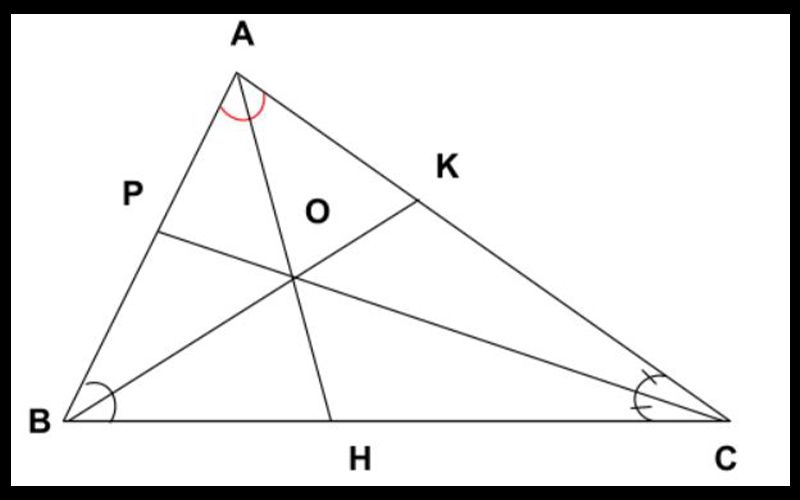
Trường hợp 2 cạnh tỉ lệ C.C.C

Đối với trường hợp tỉ lệ cạnh – cạnh – cạnh (viết tắt là c.c.c) thì ta có phát biểu sau đây:

Nếu ba cạnh của một tam giác bất kỳ tỉ lệ với ba cạnh của một tam giác khác thì hai tam giác này được gọi là đồng dạng với nhau, theo trường hợp cạnh – cạnh – cạnh.

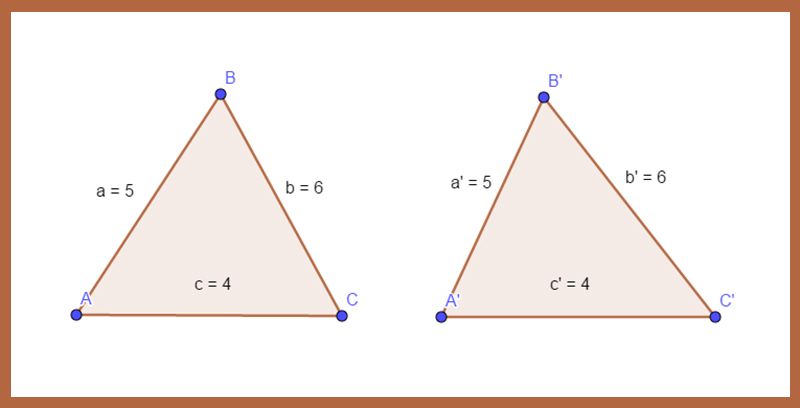
Trường hợp góc và 2 cạnh liền kề C.G.C

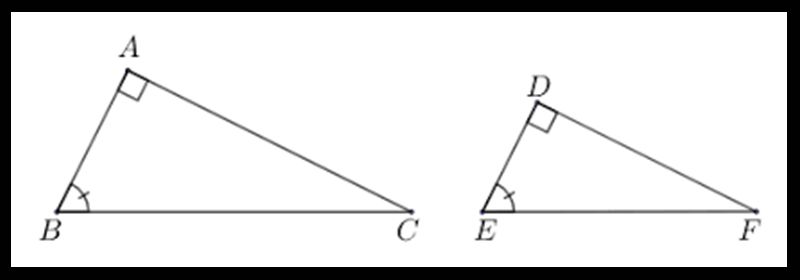
Trường hợp cạnh – góc – cạnh (chỉ xét một góc và hai cạnh kề của góc đó) thì ta có phát biểu như dưới đây:

Nếu hai cạnh của một tam giác này tỉ lệ với hai cạnh của tam giác khác, và hai góc được tạo bởi hai cặp cạnh này bằng nhau thì hai tam giác đó được gọi là đồng dạng với nhau, theo trường hợp cạnh – góc – cạnh.

Trường hợp 3 góc bằng nhau G.G.G

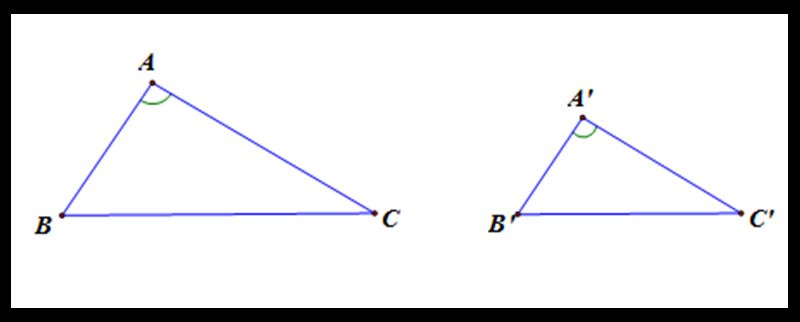
Một trường hợp khác của tam giác đồng dạng mà ta cũng cần ghi nhớ, đó là trường hợp góc – góc (hay còn gọi là g.g). Đối với trường hợp này, ta có phát biểu như sau:

Nếu hai góc của một tam giác bất kỳ lần lượt bằng hai góc của một tam giác khác thì ta nói, hai tam giác này đồng dạng với nhau, theo trường hợp góc – góc.

Dạng bài tập về tam giác đồng dạng

Sau đây là một số dạng bài tập thường gặp có liên quan đến tam giác đồng dạng. Các bạn có thể tham khảo để ôn tập và chuẩn bị cho những kỳ thi sắp tới.

• Bài tập 1: Cho △ABC và △A’B’C’. △ABC ∼ △A’B’C’ khi:

A. Góc A = góc A’, góc B = góc B’

B. Góc A = góc B, góc A’ = góc B’

C. Góc A = góc C, góc A’ = góc C’

D. Tất cả các trường hợp trên đều sai

Đáp án: A. Góc A = góc A’, góc B = góc B’

• Bài tập 2: Phát biểu nào dưới đây là sai?

A. Mỗi tam giác đều đồng dạng với chính nó

B. Nếu △ABC ∼ △A’B’C’ thì ngược lại, △A’B’C’ ∼ △ABC

C. Trong một tam giác thì đường phân giác của một góc bất kỳ sẽ chia cạnh đối diện thành hai đoạn thẳng không tỉ lệ với hai cạnh kề của hai đoạn ấy

D. k được gọi là tỉ số đồng dạng khi k = A’B/AB = B’C’/BC = A’C’/AC

Đáp án: C. Trong một tam giác thì đường phân giác của một góc bất kỳ sẽ chia cạnh đối diện thành hai đoạn thẳng không tỉ lệ với hai cạnh kề của hai đoạn ấy

• Bài tập 3: Cho ΔABC vuông tại A

  có AB = 3cm, BC = 5cm và ΔA

  1

  B

  1

  C

  1

   vuông tại B

  1

   có A

  1

  B

  1 

  = 6cm, B

  1

  C

  1 

  = 8cm. Hai tam giác vuông ΔABC và ΔA

  1

  B

  1

  C

  1

   có đồng dạng với nhau không? Vì sao?

Đáp án:

ΔABC vuông tại A có AC2 = BC2 – AB2 = 25 – 9 = 16 => AC = 4 (cm).

Tương tự, ΔA1B1C1 vuông tại B1 có (A1C1)2 = (A1B1)2 + (B1C1)2 = 36 + 64 = 100 => A1C1 = 10 (cm)

Ta có: AB/A1B1 = 3/6 = 1/2, CA/C1B1 = 4/8 = 1/2, CB/C1A1 = 5/10 = 1/2

=> AB/A1B1 = CA/C1B1 = CB/C1A1

Vậy ta nói, hai tam giác vuông ΔABC và ΔA1B1C1 đồng dạng với nhau theo trường hợp cạnh – cạnh – cạnh.

• Bài tập 4: ΔABC có AB = 12cm, AC = 15cm, BC = 18cm. Trên cạnh AB lấy điểm M sao cho AM = 10cm. Trên cạnh AC lấy điểm N sao cho AN = 8cm.

a. Tam giác AMN đồng dạng với tam giác nào?

b. Tính độ dài MN.

Đáp án:

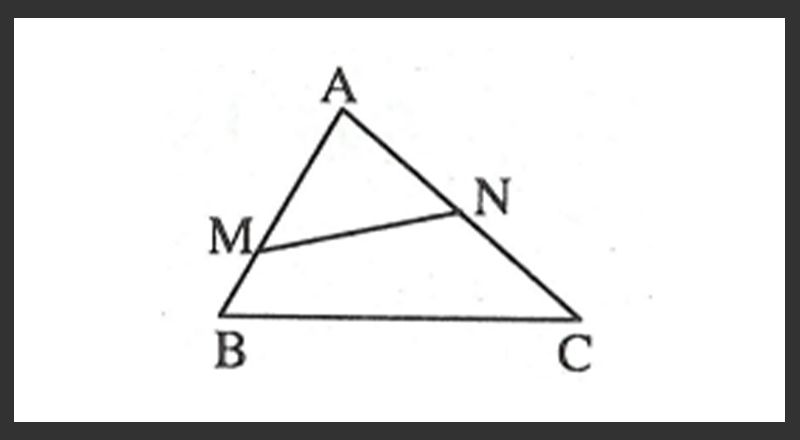
a. Ta có: AM/AC = 10/15 = 2/3, góc A chung, AN/AB = 8/12 = 2/3

=> ΔAMN đồng dạng với ΔACB theo trường hợp cạnh – góc – cạnh.

b. Vì ΔAMN đồng dạng với ΔACB nên MN/CB = AM/AC

=> MN = AM.CB/AC = 10.18/14 = 12 (cm)

Vậy MN = 12 cm.

• Bài tập 5: Cho hình thang ABCD có AB // CD. Gọi O

  là giao điểm của hai đường chéo AC và BD.

  Chứng minh rằng OA.OD = OB.OC.

Đáp án:

Vì AB // CD => Góc OAB = góc OCD (so le trong).

Tam giác OAB và tam giác OCD có: Góc AOB = góc COD, góc OAB = góc OCD

=> tam giác OAB đồng dạng với tam giác OCD

=> OA/OC = OB/OD = AB/CD

=> OA.OD = OB.OC.

Xem thêm: 

Trên đây là một số thông tin về khái niệm, tính chất và các trường hợp tam giác đồng dạng thường gặp trong toán học. Các bạn có thể tham khảo một số dạng bài tập ở trên để ôn luyện cho những kỳ kiểm tra sắp tới. Chúc các bạn gặt hái được kết quả cao trong các môn học.