Dueling Network Architectures for Deep Reinforcement Learning

This repository provides the Pytorch implementation of Dueling Network Architectures for Deep Reinforcement Learning paper

Authors: Ziyu Wang, Tom Schaul, Matteo Hessel, Hado van Hasselt, Marc Lanctot, Nando de Freitas

Link to the paper: https://arxiv.org/pdf/1511.06581.pdf

Overview

This paper presents a complete new network architecture for the model-free reinforcement learning layered over the existing architectures. This dueling network represents two separate estimates, one for the state value function and another for the action advantage function. The main benefit of separating estimates is that the agent can learn over the actions without imposing any change in the basic reinforcement learning algorithm. It is an alternative but complementary approach of focusing primarily on innovating a neural network architecture which provides more better results for model-free RL. This dueling algorithm outperforms the state-of-the-art on the Atari 2600 domain.

In the implementation, I have used both the Q-Network algorithms, DeepQNetwork and improvised DoubleDeepQNetwork (similar to the DeepQNetwork with a small update in the output value y) of van Hasselt et al. (2015). I have also used an experience replay memory which improves the algorithm more better as the experience tuples can provide high expected learning progress and also leads to faster learning and better policy. I have currently used the random policy for getting a experience from the replay memory (prioritized replay even performs better).

For choosing any action at a particular state, I have used the epsilon-greedy policy specified as below:

The dueling network architecture now considers the action value function as the combination of the value and the advantage functions. The paper first starts with the addition of value and advantage but that had an issue of identifiability (adding some constant to value and subtracting same from advantage results in same Q value). To address this, paper says to force the advantage estimator function to have zero advantage at the chosen action. The equation looks as follows:

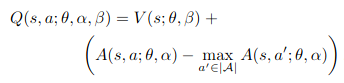
I have used an alternative equation (mentioned in the paper) which replaces the max operator in the above equation to average of all the advantages. Also, this makes the equation linear. Here’s the equation used:

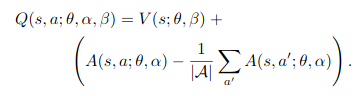
As dueling network shares the same input-output interface as the simple Q-networks, all the learning algorithms of Q-networks can be used for training the dueling architecture.

Setup

Prerequirements

• Python
• Numpy
• OpenAI gym
• Pytorch
• Matplotlib (for plotting the results)
  For installing all the requirements just run the requirements.txt file using the following command:

pip3 install -r requirements.txt  

Running the pre-trained model

• Just run the main.py file by the command python main.py with making the load_checkpoint variable to True which will load the saved parameters of the model and output the results.

Training the model

• You can train the model by running the main.py file using the command
  python main.py– You can set the number of games for training by changing the value of variable n_games (current is 500) in main.py.
• You can set the hyper-parameters such as learning_rate, discount factor (gamma), epsilon, and others while initializing the agent variable in main.py.
• You can set the desired path for the checkpoint saving by changing the checkpoint_dir variable and for the plot saving by changing the plot_path variable.
• The environment can be changed by updating the parameter of the make_env while initializing env variable in main.py. Default is the Pong environment.
• You can train the model using the DuelingDeepQNetwork or DuelingDoubleDeepQNetwork by changing the agent variable initialization as per the need.

File Structure

• main.py – Performs the main work of running the model over the number of games for learning with initializing the agents, calculating different result statistics, and plotting the results.
• DuelingDeepQNetwork.py – Contains the complete architecture of converting the input frame (in form of an array) to getting the outputs (value and advantage functions). It contains the 3 convolution layers (with ReLU function applied) followed by two fully connected (with ReLU) outputing the value and advantage. It also has the optimizer, and loss function.
• DuelingDQNAgent.py – This file provides agent for the DuelingDeepQNetwork containing the main learning function. With this, it also contains methods for changing epsilon, getting samples, storing experiences, choosing actions (using epsilon-greedy approach), replacing target networks, etc.
• DuelingDDQNAgent.py – This file provides agent for the DuelingDoubleDeepQNetwork having major things similar to the DuelingDQNAgent with some changes in the learn function.
• ExperienceReplayMemory.py – This file contains the past experiences observed by the agent while playing the games which becomes useful in learning. It contains the methods for adding an experience, and getting any random experience.
• utils.py – This file contains the code for building the environment of the Atari game with methods for preprocessing frames, stacking frames, etc. needed to make it similar to the DeepMind paper.
• results/ – This folder contains the saved models learnt by DuelingDeepQNetwork and DuelingDoubleDeepQNetwork.
• images/ – This folder contains the images used in this README.
• README.md – This file which gives complete overview of the implementation.
• requirements.txt – Provides ready to install all the required libraries for running the implementation.

Dueling Architecture

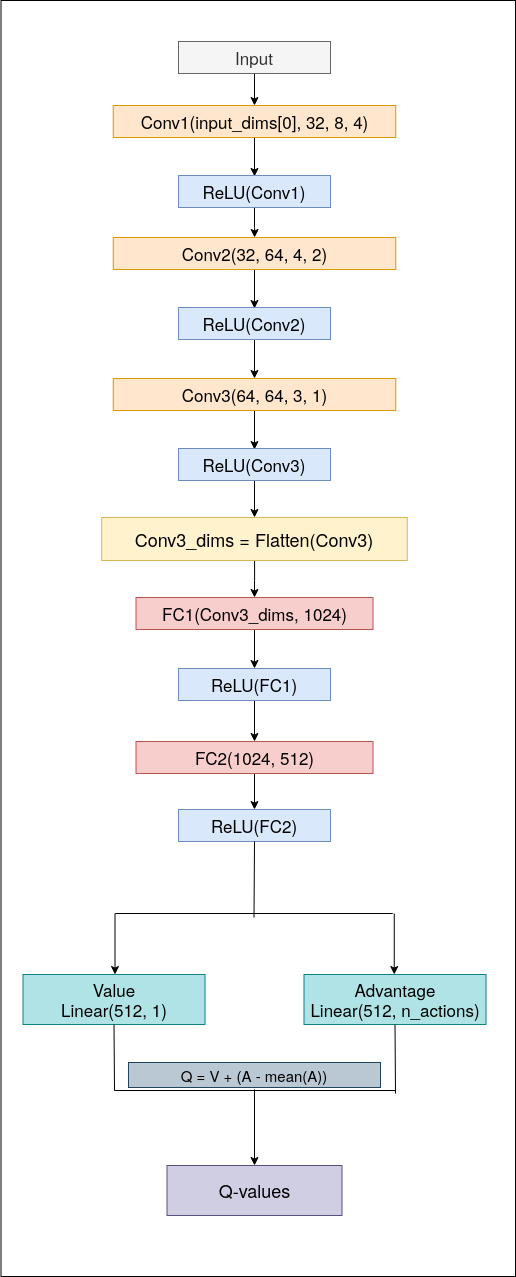
The architecture of the Dueling Deep Q Network is quite simple with just one important thing of taking two outputs from the same neural network (instead of one). Here, basically the input_dimensions are passed to the network which are convoluted using three convolution layers with each following the ReLU (Rectified Linear Unit) activation. The first convolution layer convolutes the input to 32 output channels with kernel size of 3 x 3 and stride of 4. The second convolution convolutes the output from the first one into 64 output channels with kernel size of 4 x 4 and stride of 2. The final convolution layer convolutes the 64 channels from the second one to 64 output channels again but with a kerner size of 3 x 3 and stride of 1.

This convoluted outputs are then flattened and passed into the fully connected layers. The first layer applies linear transformation from the flattened outputs dimensions to 1024 which is again linearly transformed to 512 by the next layer. This 512 neurons are then linearly transformed into two outputs separately: value (from 512 to 1) and advantage (from 512 to the number of actions) function.

These value and advantage functions are then used to calculate the Q value of the learning function basically described as below

Q_value = Value + (Advantage - mean(Advantage))  

Results

Both the architectures provided good results of winning with a scores up to 20-22 in Pong game (PongFrameskip-v4) by learning over 1000 games. Here are the learning plots of both the algorithms with scores averaged over last 30 to avoid high fluctuations:

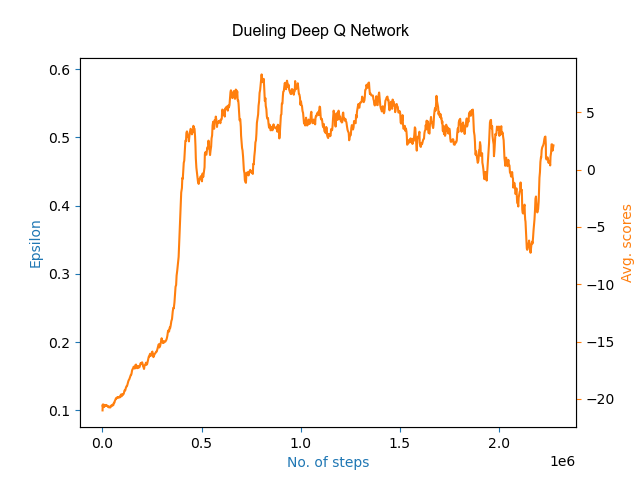
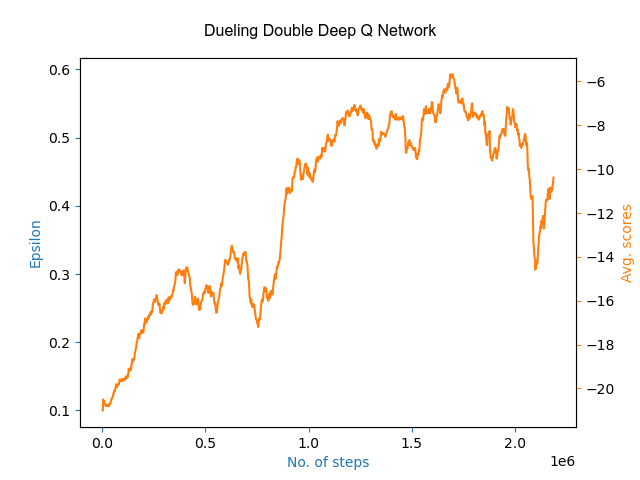
Here, the high fluctuations in between the plots shows that the agent explores instead of choosing any greedy action which may result in some better policy.

Note: You can view the plot with each scores at DuelingDeepQNetwork and DuelingDoubleDeepQNetwork.

Observations

The DuelingDeepQNetwork as well as DuelingDoubleDeepQNetwork agents were trained for 1000 games with storing the scores, epsilon, and steps count. The hyperparameters which provided good results after training are as follows:

Learning Rate
0.0001

Epsilon (at start)
0.6

Gamma (discount factor)
0.99

Dec epsilon
1e-5

Min epsilon
0.1

Batch size
32

Replay Memory Size
1000

Network replace count
1000

Dec epsilon
1e-5

Input dimensions
Shape of observation space

n_actions
Taken from action space of environment

Note: The paper describes starting epsilon value as 1.0 which performs better when training for a lot of steps (about 50 million). While here, I have decreased the starting epsilon, i.e., exploration, to 0.6 as for 1000 games, it runs nearly for only million steps.

References