Giải bài 1,2,3,4,5, 6,7,8,9 trang 17 SGK hình học 10: Tích của véctơ với một số

Tóm tắt kiến thức và Giải bài 1,2,3,4,5, 6,7,8,9 trang 17 SGK hình học 10: Tích của véctơ với một số – Chương 1 hình 10.

A. Tóm tăt kiến thức Tích của véctơ với một số

1. Định nghĩa 

Cho một số ít k # 0 và vec tơ → a # → 0

Tích của một số k với vec tơ →a  là một vec tơ, kí hiệu là k→a
cùng hướng với →a  nếu k > 0, ngược hướng với →a   nếu k< 0 và có độ dài bằng |k|. |→a |

2. Tính chất : Tích của một số với một vec tơ có tính chất:

a ) Phân phối với phép cộng vec tơ : k ( → a + → b ) = k → a + k → b
b ) Phân phối với phép cộng những số : ( h + k ) → a = h → a + k → a
c ) Kết hợp : h ( k → a ) = ( h. k ) → a .
d ) 1. → a = → a ( – 1 ) → a = – → a

3.Áp dụng

a ) Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có → MA + → MB = 2 → MI .
b ) Nếu G là trọng tâm của tam giác ABC thi mọi điểm M ta có
→ MA + → MB + → MC = 3 → MG .

4. Điều kiện để hai vec tơ cùng phương

Điều kiện cần và đủ để hai vec tơ cùng phương là có 1 số ít k để → a = k → b .Quảng cáo

5. Phân tích một vec tơ thành haivec tơ không cùng phương

Cho hai vec tơ →a  và →b không cùng phương. Khi đó một vec tơ →x  đều hân tích được một cách duy nhất theo hai vec tơ →a , →b
nghĩa là có duy nhất một cặp số h, k sao cho →x =  h→a + k→b

B. Hướng dẫn giải bài tập Tích của véctơ với một số trang 17 Hình học lớp 10

Bài 1. Cho hình bình hành ABCD. Chứng minh rằng: →AB + →AC + →AD = 2→AC.

Giải: →AB + →AC + →AD = →AB + →AD + →AC

ABCD là hình bình hành nên → AB + → AD = → AC ( quy tắc hình bình hành của tổng )
⇒ → AB + → AC + → AD = → AC + → AC = 2 → AC

Bài 2. Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ →AB, →BC, →AC theo hai vectơ sau →u = →AK, →v = →BM.

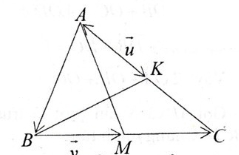
Vì M là trung điểm của BC nên  →BC = 2 →BM = 2 →v;
Vì K là trung điểm của CA nên  →CA = -2 →AK = -2 →u;
Ta có:  →CB = – →BC = -2 →v
nên  →AB =  →CB –  →CA = -2 →v – (-2 →u) =2( →u- →v).

Bài 3. Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho →MB = 3→MC . Hãy phân tích vectơ  →AM  theo hai vectơ →u  = →AB , →v  = →AC.

Ta có: →AM = →AB + →BM = →AB + →BC + →CM
Vì →MB = 3→MC nên →BM = 3→CM

Quảng cáo

⇒ →BC = 2→CM ⇒ →CM =1/2 →BC
Từ đó: →AM = →AB +3/2 →BC
Mặt khác →BC = →AC – →AB = →v – →u
Khi đó: →AM = →AB + 3/2 →BC = →u +3/2 (→v – →u) = 3/2→v -1/2 →u.

Bài 4. Gọi AM là trung tuyến của tam giác ABC  và D là trung điểm của đạn AM. Chứng minh rằng:

a ) 2 → DA + → DB + → DC = → 0 ;
b ) 2 → OA + → OB + → OC = 4 → OD, với O là điểm tùy ý .

Giải bài 4: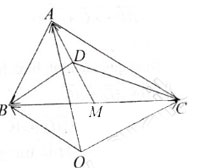

a) Ta có:
→DB + →DC = (→DM + →MB) + (→DM + →MC) = 2 →DM + (→MB + →MC) = 2 →DM + →0 = 2→DM (vì →MB = –→MC).
Mặt khác, do D là trung điểm của đoạn AM nên →DM = – →DA.
Khi đó: 2→DA + →DB + →DC = 2→DA + 2→DM =2 (→DA +→DM) = →0

b) Ta có:
2→OA + →OB + →OC = 4 →OD ⇔ 2(→OA – →OD) + (→OB –→OD) + (→OC – →OD) = 0
⇔ 2DA + DB + DC= 0 (luôn đúng theo câu a)
Vậy 2→OA +→OB+ →OC = 4→OD, với O là điểm tùy ý.

Bài 5 trang 17 Hình 10. Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng:   2→MN= →AC + →BD = →BC + →AD.

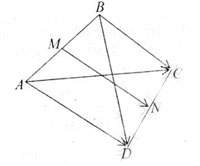Ta có: →AC = →AM + →MN + →NC→BD = →BM + →MN + →ND
→AC +→BD = 2→MN + (→AM + →BM) + (→NC +→ND)
=2→MN + →0 + →0 = 2→MN
(Vì BM = – AM; ND = -NC)
Tương tự, từ: →BC = →BM + →MN + →NC
→AD = →AM + →MN + →ND
Ta suy ra: →BC + →AD = 2 →MN. Vậy 2 →MN = →AC + →BD =→ BC + →AD.

Bài 6. Cho hai điểm phân biệt A và B. Tìm điểm K sao cho  3→KA + 2 →KB = →0

Giải: Ta có:  →KA + 2 →KB = →0  ⇒ 3→KA = -2 →KB ⇒→KA = – 2/3 →KB
Đẳng thức này chứng tỏ hai vec tơ  →KA ,→KB là hai vec tơ ngược hướng, do đó K thuộc đoạn AB

Ta lại có : | → KA | = – 2/3 | → KB | ⇒ KA = 2/3 KB
Vậy K là điểm chia trong đoạn thẳng AB theo tỉ số 2/3 .

Bài 7 trang 17. Cho tam giác ABC. Tìm điểm m sao cho →MA + →MB +2 →MC = →0

Giải: Gọi I là trung điểm của AB; J là trung điểm của CI
Ta có, theo quy tắc hình bình hành:  →MA + →MB = 2 →MI. Khi đó: →MA + →MB + 2→MC = →0 ⇔2 →MI + 2 →MC = →0 ⇔2(→MI + →MC) = →0;
Cũng theo quy tắc hình bình hàng: →MI + →MC = 2→MJ
Do đó 2(→MI + →MC) = 0 ⇔ 4→MJ = 0 ⇔ →MJ = 0 ⇔ M=J
Vậy M là trung điểm của CI.

Bài 8. Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

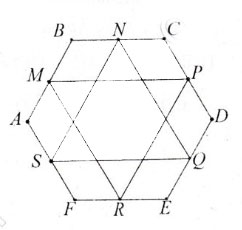
Ta có: →MN =1/2 →AC
→PQ =1/2 →CE
→RS=1/2 →EA

⇒ →MN + →PQ + →RS = 1/2(→AC + →CE + →EA) = 1/2 →AA = →0
⇒ →MN + →PQ + →RS = →0 (1)
Gọi G là trọng tâm tam giác MPR, ta có:
→GM + →GP + →GR = →0 (2)
Mặt khác →MN = →MG +→ GN
→PQ =→ PG + →GQ
→RS = →RG + →GS
⇒ →MN +→ PQ + →RS = (→MG + →PG +→ RG) + →GN + →GQ + →GS (3)
Từ (1),(2),(3) suy ra: →GN + →GQ + →GS = →0
Vậy G là trọng tâm của tam giác NQS.

Bài 9 trang 17 Toán Hình 10. Cho tam giác đều ABC có trọng tâm O và M là một điểm tùy ý trong tam giác. Gọi D,E,F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng:→MD + →ME + →MF = 3/2→MO.

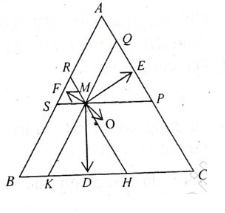
Từ M kẻ SP//BC; HR//CA và KQ//AB. Ta có:

+ ΔMKH đều: MD là đường trung tuyến ⇒ 2→MD = →MK + →MH
+ ΔMPQ đều: ME là đường trung tuyến ⇒ 2→ME = →MP + →MQ
+ ΔMRS đều: MF là đường trung tuyến ⇒ 2→MF = →MR + →MS

⇒ 2(→MD + →ME + →MF) = →MH + →MK + →MP + →MQ + →MR + →MS
=(→MQ + →MR) + (→MS + →MK) + (→MH + →MP) = →MA + →MB + →MC
(Vì các tứ giác MHCP, MQAR, MSBK là các hình bình hành)
Vì O là trọng tâm của ΔABC nên →MA + →MB + →MC = 3 →MO
Từ đó: 2(→MD + →ME + →MF ) = 3 →MO

⇒ → MD + → ME + → MF = 3/2 → MO ( đpcm )

Source: https://evbn.org
Category : blog Leading