Bài Tập Về Sự Đồng Biến Nghịch Biến Của Hàm Số Hay Nhất
1/5 – (1 vote)
Bài tập về sự đồng biến nghịch biến của hàm số là phần khá quan trọng trong chương trình toán 12. Hãy cùng WElearn gia sư tìm hiểu về bài tập này nhé!
>>>> Xem thêm: Gia sư dạy kèm tại nhà môn Toán
Mục Lục
1. Hệ thống lại kiến thức
1.1. Định nghĩa tính đơn điệu của hàm số
Cho hàm số y = f(x) xác định trên K (với K là một khoảng hoặc một đoạn hoặc nửa khoảng).
- Hàm số y = f(x) là đồng biến (tăng) trên (nếu với mọi x1, x2 thuộc K, x1 < x2 => f(x1) < f(x2).
- Hàm số y = f(x) là nghịch biến (giảm) trên K (nếu với mọi x1, x2 thuộc K, x1 < x2 => f(x1) > f(X2). Hàm đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
1.2. Điều kiện cần và đủ để hàm số đơn điệu
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
- Nếu hàm số đồng biến trên khoảng K thì f’(x) ≥ 0, với mọi x thuộc K và f’(x) = 0 xảy ra tại một số hữu hạn điểm.
- Nếu hàm số nghịch biến trên khoảng K thì f(x) ≤ 0, với mọi x thuộc K và f’(x) = 0 xảy ra tại một số hữu hạn điểm.
1.3. Phương pháp xét tính đơn điệu của hàm số
- Bước 1: Tìm tập xác định.
- Bước 2: Tính đạo hàm f’(x). Tìm các điểm xi(i=1,2,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
2. Bài tập
Câu 1: Cho đồ thị hàm số với x ∈ [- π/2 ; 3π/2] như hình vẽ.

Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- π/2 ; 3π/2]

Câu 2: Cho đồ thị hàm số y = -x3 như hình vẽ. Hàm số y = -x3 nghịch biến trên khoảng:
A. (-1;0) B. (-∞;0) C. (0;+∞) D. (-1;1)

Câu 3: Cho đồ thị hàm số y = -2/x như hình vẽ. Hàm số y = -2/x đồng biến trên

A. (-∞;0) B. (-∞;0) ∪ (0;+∞) C. R D. (-∞;0) và (0;+∞)
Câu 4: Khoảng nghịch biến của hàm số y = x3/3 – 2×2 + 3x + 5 là:
A. (1;3) B.(-∞; 1) ∪ (3; +∞) C. (-∞; 1) và (3; +∞) D. (1;+∞)
Câu 5: Cho hàm số y = x4 – 2×2 + 3 . Kết luận nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)
B. Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)
C. Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)
D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)
Câu 6: Cho hàm số y = x3 + 3×2 + mx + 1 – 2m. Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
A. m =0 B. m = ¼ C. 9/4 D. Không tồn tại
Câu 7: Cho hàm số y = sin2x – 2x. Hàm số này
A. Luôn đồng biến trên R B. Chỉ đồng biến trên khoảng (0; +∞)
C. Chỉ nghịch biến trên (-∞; -1) D. Luôn nghịch biến trên R
Câu 8: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?
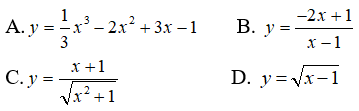
Câu 9: Tìm m để hàm số

luôn nghịch biến trên khoảng xác định.
A.-2 < m ≤ 2 B. m < -2 hoặc m > 2 C. -2 < m < 2 D. m ≠ ±2
Câu 10: Cho hàm số y = -x3 + 3×2 + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m < 1 B. m ≥ 1 C. m ≤ -1 D. m ≥ -1
Câu 11: Cho đồ thị hàm số có dạng như hình vẽ.
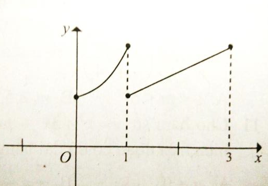
Hàm số đồng biến trên:
A. (0;1) B. (1;3) C. (0; 1) ∪ (1; 3) D. (0;1) và (1;3).
Câu 12: Hỏi hàm số đồng biến trên các khoảng nào?

A. (-∞ ; +∞) B. (-∞; -5) C. (-5; +∞) ∪ (1; 3) D. (0; 1) và (1; 3)
Câu 13: Tìm khoảng đồng biến của hàm số y = 2×3 – 9×2 + 12x + 3
A.(-∞; 1) ∪ (2; +∞) B. (-∞ 1] và [2; +∞) C. (-∞; 1) và (2; +∞) D. (1;2)
Câu 14: Khoảng nghịch biến của hàm số y = x4 – 2×2 – 1 là:
A. (-∞; -1) và (0; 1) B. (-∞; 0) và (1; +∞) C. (-∞; -1) ∪ (0; 1) D. (0;1)
Câu 15: Cho hàm số
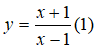
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số (1) nghịch biến trên R\{1}
B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)
C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)
D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Câu 16: Tìm khoảng đồng biến của hàm số f(x)= x + cos2x
A. R\{0} B. (-∞; +∞) C. (-1; 1) D. (0; π)
Câu 17: Hàm số:
![]()
đồng biến trên khoảng nào?
A. R B. (-∞; 0) C. (-1; 0) D. (0; +∞)
Câu 18: Cho hàm số y = x3 – x2 + (m-1)x + m. Tìm điều kiện của tham số m để hàm số đồng biến trên R
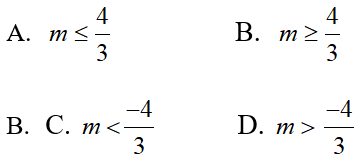
Câu 19: Cho hàm số
![]()
Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).
A. m < 2√2 B. m ≥ -2√2 C. m = 2√2 D. -2√2 ≤ m 2√2
Câu 20: Tìm tất cả các giá trị của tham số m sao cho hàm số

A. 1 < m < 5 B. m ≥ 5 C. m < -1 hoặc m > 5 D. m > 5
Đáp án
- A
- C
- D
- A
- D
- D
- D
- C
- C
- C
- C
- B
- C
- C
- D
- B
- A
- B
- C
- D
Như vậy, với những tóm tắt và Bài Tập Về Sự Đồng Biến Nghịch Biến Của Hàm Số Hay Nhất, hy vọng các bạn có thể làm chủ môn toán nhé!
Xem thêm những bài viết tương tự















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


