VBT Toán lớp 9 Bài 2: Hàm số bậc nhất| Giải VBT Toán lớp 9

Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 2: Hàm số bậc nhất trang 55,56,57 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 2: Hàm số bậc nhất

Phần câu hỏi bài 2 trang 55 Vở bài tập toán 9 tập 1

Câu 3

Trong các hàm số dưới đây, hàm số không phải là hàm số bậc nhất là:

(A) y=1–5x      

(B) y=−0,5x

(C) y=2(x−1)+3

(D) y=2×2+3

Phương pháp giải:

Sử dụng khái niệm về hàm bậc nhất, kiểm tra các hàm số đã cho rồi chọn đáp án đúng nhất.

Hàm số bậc nhất là hàm số được cho bởi công thức y=ax+b, trong đó a,b là các số cho trước và a≠0.

Trả lời:

A. Hàm số bậc nhất có a=−5 và b=1

B. Hàm số bậc nhất có a=−0,5 và b=0

C. Hàm số bậc nhất có a=2 và b=3−2

D. Không phải là hàm số bậc nhất.

Đáp án cần chọn là D.

Câu 4

Hàm số y=(35−m)x+13 là hàm số đồng biến trên R khi:

 (A) m=23                                (B) m=−15

(C) m=45                                  (D) m=1

Phương pháp giải:

Sử dụng kiến thức hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và đồng biến trên R khi a > 0.

Trả lời:

Hàm số y=(35−m)x+13 là hàm số đồng biến trên R khi 35−m>0⇔m<35

Ta có : −15<35

Đáp án cần chọn là B.

Câu 5

Hàm số y=(k−23)x−12 là hàm số nghịch biến trên R khi:

(A) k=34                                  (B) k=56

(C) k=45                                   (D) k=12 

Phương pháp giải:

Vận dụng kiến thức : Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và nghịch biến trên R khi a < 0.

Trả lời:

Hàm số y=(k−23)x−12 là hàm số nghịch biến trên R khi k−23<0⇔k<23

Vì 12<23 nên đáp án cần chọn là D.

Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số:

a) Đồng biến

b) Nghịch biến

Phương pháp giải:

Vận dụng kiến thức : Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:

a) Đồng biến trên R khi a > 0

b) Nghịch biến trên R khi a < 0

Trả lời

a) Hàm số: y=(m−2)x+3 đồng biến khi m−2>0⇔m>2

Vậy m>2 thì hàm số đã cho đồng biến trên R 

b)  Hàm số: y=(m−2)x+3 nghịch biến khi m−2<0⇔m<2

Vậy m<2 thì hàm số đã cho nghịch biến trên R

Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của nó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x.

Phương pháp giải:

– Biểu diễn chiều dài và chiều rộng của hình chữ nhật khi giảm đi x (cm)

– Viết công thức tính chu vi hình chữ nhật rồi biến đổi để được công thức tính y theo x.

Trả lời:

Các kích thước của hình chữ nhật mới là 20−x và 30−x(cm)

Công thức tính chu vi y của hình chữ nhật mới là :

y=2(20−x+30−x)=2(50−2x)=100−4x

Vậy y=100−4x là công thức cần tìm.

Hãy biểu diễn các điểm sau trên mặt phẳng tọa độ: A(−3;0),B(−1;1),C(0;3),D(1;1),E(3;0),F(1;−1),G(0;−3),H(−1;−1).

Phương pháp giải:

Biểu diễn điểm M(x0;y0) trên mặt phẳng tọa độ ta làm như sau :

– Vẽ đường thẳng song song với trục tung Oy tại hoành độ x=x0.

– Vẽ đường thẳng song song với trục hoành Ox tại tung độ y=y0.

– Giao điểm của hai đường thẳng trên chính là điểm M(x0;y0).

Ghi nhớ : Những điểm trên trục hoành có tung độ y0=0 và những điểm trên trục tung có hoành độ x0=0.

Trả lời:

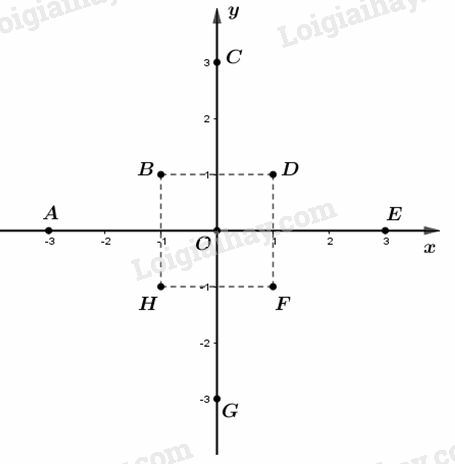
+) Điểm A(−3;0)⇒ hoành độ là −3 và tung độ là 0

⇒ điểm A nằm trên trục hoành, tại vị trí điểm −3.

+) Điểm B(−1;1)⇒ hoành độ là −1 và tung độ là 1

+) Điểm C(0;3)⇒ hoành độ là 0 và tung độ là 3

⇒ điểm C nằm trên trục tung, tại vị trí điểm 3.

+) Điểm D(1;1)⇒ hoành độ là 1 và tung độ là 1

+) Điểm E(3;0)⇒ hoành độ là 3 và tung độ là 0

⇒ điểm E nằm trên trục hoành, tại vị trí điểm 3.

+) Điểm F(1;−1)⇒ hoành độ là 1 và tung độ là −1

+) Điểm G(0;−3)⇒ hoành độ là 0 và tung độ là −3

⇒ điểm C nằm trên trục tung, tại vị trí điểm −3.

+) Điểm H(−1;−1)⇒ hoành độ là −1 và tung độ là −1

Bài 9 trang 57 Vở bài tập toán 9 tập 1:

Với những giá trị nào của m thì mỗi hàm số sau là hàm số bậc nhất ?

a) y=5−m(x−1).

b) y=m+1m−1x+3,5

Phương pháp giải:

Vận dụng kiến thức : Hàm số bậc nhất là hàm số được cho bởi công thức  trong đó  là các số cho trước và .

Trả lời:

a) Ta viết hàm số đã cho dưới dạng (y=ax+b) quen thuộc: y=5−m(x−1)=5−m.x−5−m

Hàm số đã cho là hàm số bậc nhất khi các số đã cho (a,b) phải xác định, và trong đó hệ số của x phải khác 0.

5−m xác định và khác 0 khi 5−m>0⇔m<5

Trả lời: Khi m<5 thì y=5−m(x−1) là hàm số bậc nhất.

b) Hàm số y=m+1m−1x+3,5 là hàm số bậc nhất khi m+1m−1 xác định và khác 0. Muốn vậy, ta phải có m+1≠0 và m−1≠0

Suy ra:m≠1 và m≠−1. Viết gộp lại là m≠±1.

Bài 10 trang 57 Vở bài tập toán 9 tập 1: Cho hàm số bậc nhất y=(1−5)x−1

a) Hàm số trên là đồng biến hay nghịch biến ? Vì sao ?

b) Tính giá trị của y khi x=1+5

c) Tính giá trị của x khi y=5

Phương pháp giải:

a) Vận dụng kiến thức : Hàm số bậc nhất y=ax+b xác định với mọi giá trị của x thuộc R và đồng biến trên R khi a>0 và nghịch biến trên R khi a<0.

b) Để tính giá trị của hàm số y=f(x) tại x=a ta thay x=a vào f(x) và viết là f(a)

c) Để tìm x khi y=5 thì thay giá trị của y vào hàm số rồi giải bài toán tìm x.

Trả lời:

a) Hàm số bậc nhất y=(1−5)x−1 là nghịch biến trên R vì a=1−5<0.

b) Khi x=1+5 thì giá trị của y là :

y=(1+5)(1−5)−1=1−5−1=−5

c) Khi y=5 thì (1−5)x−1=5 ⇒x=1+51−5=(1+5)(1+5)(1−5)(1+5)=(1+5)2−4=6+25−4=−3+52