TensorFlow 2 Tutorial: Get Started in Deep Learning with tf.keras – MachineLearningMastery.com
Last Updated on August 2, 2022
Predictive modeling with deep learning is a skill that modern developers need to know.
TensorFlow is the premier open-source deep learning framework developed and maintained by Google. Although using TensorFlow directly can be challenging, the modern tf.keras API brings Keras’s simplicity and ease of use to the TensorFlow project.
Using tf.keras allows you to design, fit, evaluate, and use deep learning models to make predictions in just a few lines of code. It makes common deep learning tasks, such as classification and regression predictive modeling, accessible to average developers looking to get things done.
In this tutorial, you will discover a step-by-step guide to developing deep learning models in TensorFlow using the tf.keras API.
After completing this tutorial, you will know:
- The difference between Keras and tf.keras and how to install and confirm TensorFlow is working
- The 5-step life-cycle of tf.keras models and how to use the sequential and functional APIs
- How to develop MLP, CNN, and RNN models with tf.keras for regression, classification, and time series forecasting
- How to use the advanced features of the tf.keras API to inspect and diagnose your model
- How to improve the performance of your tf.keras model by reducing overfitting and accelerating training
This is a lengthy tutorial and a lot of fun. You might want to bookmark it.
The examples are small and focused; you can finish this tutorial in about 60 minutes.
Kick-start your project with my new book Deep Learning With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Update Jun/2020: Updated for changes to the API in TensorFlow 2.2.0.

Mục Lục
TensorFlow Tutorial Overview
This tutorial is designed to be your complete introduction to tf.keras for your deep learning project.
The focus is on using the API for common deep learning model development tasks; you will not be diving into the math and theory of deep learning. For that, I recommend starting with this excellent book.
The best way to learn deep learning in Python is by doing. Dive in. You can circle back for more theory later.
Each code example was designed to use best practices and to be standalone so that you can copy and paste it directly into your project and adapt it to your specific needs. This will give you a massive head start over trying to figure out the API from the official documentation alone.
It is an extensive tutorial, and as such, it is divided into five parts; they are:
- Install TensorFlow and tf.keras
- What Are Keras and tf.keras?
- How to Install TensorFlow
- How to Confirm TensorFlow Is Installed
- Deep Learning Model Life-Cycle
- The 5-Step Model Life-Cycle
- Sequential Model API (Simple)
- Functional Model API (Advanced)
- How to Develop Deep Learning Models
- Develop Multilayer Perceptron Models
- Develop Convolutional Neural Network Models
- Develop Recurrent Neural Network Models
- How to Use Advanced Model Features
- How to Visualize a Deep Learning Model
- How to Plot Model Learning Curves
- How to Save and Load Your Model
- How to Get Better Model Performance
- How to Reduce Overfitting with Dropout
- How to Accelerate Training with Batch Normalization
- How to Halt Training at the Right Time with Early Stopping
You Can Do Deep Learning in Python!
Work through the tutorial at your own pace.
You do not need to understand everything (at least not right now). Your goal is to run through the tutorial end-to-end and get results. You do not need to understand everything on the first pass. Write down your questions as you go. Make heavy use of the API documentation to learn about all of the functions that you’re using.
You do not need to know the math first. Math is a compact way of describing how algorithms work, specifically the tools from linear algebra, probability, and statistics. These are not the only tools you can use to learn how algorithms work. You can also use code and explore algorithmic behavior with different inputs and outputs. Knowing the math will not tell you what algorithm to choose or how to configure it best. You can only discover that through careful, controlled experiments.
You do not need to know how the algorithms work. Knowing the limitations and how to configure deep learning algorithms is important. But learning about algorithms can come later. You need to build up this algorithm knowledge slowly over a long period of time. Today, start by getting comfortable with the platform.
You do not need to be a Python programmer. The syntax of the Python language can be intuitive if you are new to it. Just like other languages, focus on function calls (e.g., function()) and assignments (e.g., a = “b”). This will get you most of the way. You are a developer, so you know how to pick up the basics of a language quickly. Just get started and dive into the details later.
You do not need to be a deep learning expert. You can learn about the benefits and limitations of various algorithms later. There are plenty of posts that you can read later to brush up on the steps of a deep learning project and the importance of evaluating model skills using cross-validation.
1. Install TensorFlow and tf.keras
In this section, you will discover what tf.keras is, how to install it, and how to confirm that it is installed correctly.
1.1 What Are Keras and tf.keras?
Keras is an open-source deep learning library written in Python.
The project was started in 2015 by Francois Chollet. It quickly became a popular framework for developers, becoming one of, if not the most, popular deep learning libraries.
Between 2015 and 2019, developing deep learning models using mathematical libraries like TensorFlow, Theano, and PyTorch was cumbersome, requiring tens or even hundreds of lines of code to achieve the simplest tasks. The focus of these libraries was on research, flexibility, and speed, not ease of use.
Keras was popular because the API was clean and simple, allowing standard deep learning models to be defined, fit, and evaluated in just a few lines of code.
A secondary reason Keras took off was that it allowed you to use any of the range of popular deep learning mathematical libraries as the backend (e.g., used to perform the computation), such as TensorFlow, Theano, and later, CNTK. This allowed the power of these libraries to be harnessed (e.g., GPUs) with a very clean and simple interface.
In 2019, Google released a new version of their TensorFlow deep learning library (TensorFlow 2) that integrated the Keras API directly and promoted this interface as the default or standard interface for deep learning development on the platform.
This integration is commonly referred to as the tf.keras interface or API (“tf” is short for “TensorFlow“). This is to distinguish it from the so-called standalone Keras open source project.
- Standalone Keras: The standalone open source project that supports TensorFlow, Theano, and CNTK backends
- tf.keras: The Keras API integrated into TensorFlow 2
Nowadays, since the features of other backends are dwarfed by TensorFlow 2, the latest Keras library supports only TensorFlow, and these two are the same.
The Keras API implementation in Keras is referred to as “tf.keras” because this is the Python idiom used when referencing the API. First, the TensorFlow module is imported and named “tf“; then, Keras API elements are accessed via calls to tf.keras; for example:
1
2
3
4
5
# example of tf.keras python idiom
import
tensorflow
as
tf
# use keras API
model
=
tf
.
keras
.
Sequential
(
)
.
.
.
Given that TensorFlow was the de facto standard backend for the Keras open source project, the integration means that a single library can now be used instead of two separate libraries. Further, the standalone Keras project now recommends all future Keras development use the tf.keras API.
At this time, we recommend that Keras users who use multi-backend Keras with the TensorFlow backend switch to tf.keras in TensorFlow 2.0. tf.keras is better maintained and has better integration with TensorFlow features (eager execution, distribution support and other).
— Keras Project Homepage, Accessed December 2019.
1.2 How to Install TensorFlow
Before installing TensorFlow, ensure that you have Python installed, such as Python 3.6 or higher.
If you don’t have Python installed, you can install it using Anaconda. This tutorial will show you how:
There are many ways to install the TensorFlow open-source deep learning library.
The most common, and perhaps the simplest, way to install TensorFlow on your workstation is by using pip.
For example, on the command line, you can type:
1
sudo pip install tensorflow
If you prefer to use an installation method more specific to your platform or package manager, you can see a complete list of installation instructions here:
There is no need to set up the GPU now.
All examples in this tutorial will work just fine on a modern CPU. If you want to configure TensorFlow for your GPU, you can do that after completing this tutorial. Don’t get distracted!
1.3 How to Confirm TensorFlow Is Installed
Once TensorFlow is installed, it is important to confirm that the library was installed successfully and that you can start using it.
Don’t skip this step.
If TensorFlow is not installed correctly or raises an error on this step, you won’t be able to run the examples later.
Create a new file called versions.py and copy and paste the following code into the file.
1
2
3
# check version
import
tensorflow
(
tensorflow
.
__version__
)
Save the file, then open your command line and change the directory to where you saved the file.
Then type:
1
python versions.py
You should then see output like the following:
1
2.2.0
This confirms that TensorFlow is installed correctly and that you are using the same version as this tutorial.
What version did you get?
Post your output in the comments below.
This also shows you how to run a Python script from the command line. You should run all code from the command line in this manner and not from a notebook or an IDE.
If You Get Warning Messages
Sometimes when you use the tf.keras API, you may see warnings printed.
This might include messages that your hardware supports features that your TensorFlow installation was not configured to use.
Some examples on your workstation may include:
1
2
3
Your CPU supports instructions that this TensorFlow binary was not compiled to use: AVX2 FMA
XLA service 0x7fde3f2e6180 executing computations on platform Host. Devices:
StreamExecutor device (0): Host, Default Version
They are not your fault. You did nothing wrong.
These are information messages and will not prevent your code’s execution. You can safely ignore messages of this type for now.
It’s an intentional design decision made by the TensorFlow team to show these warning messages. A downside of this decision is that it confuses beginners and trains developers to ignore all messages, including those that potentially may impact the execution.
Now that you know what tf.keras is, how to install TensorFlow, and how to confirm your development environment is working, let’s look at the life-cycle of deep learning models in TensorFlow.
2. Deep Learning Model Life-Cycle
In this section, you will discover the life-cycle for a deep learning model and the two tf.keras APIs that you can use to define models.
2.1 The 5-Step Model Life-Cycle
A model has a life cycle, and this very simple knowledge provides the backbone for both modeling a dataset and understanding the tf.keras API.
The five steps in the life cycle are as follows:
- Define the model
- Compile the model
- Fit the model
- Evaluate the model
- Make predictions
Let’s take a closer look at each step in turn.
Define the Model
Defining the model requires first selecting the type of model you need and then choosing the architecture or network topology.
From an API perspective, this involves defining the layers of the model, configuring each layer with a number of nodes and activation function, and connecting the layers together into a cohesive model.
Models can be defined either with the Sequential API or the Functional API, and the next section will look at these two.
1
2
3
.
.
.
# define the model
model
=
.
.
.
Compile the Model
Compiling the model requires first selecting a loss function that you want to optimize, such as mean squared error or cross-entropy.
It also requires that you select an algorithm to perform the optimization procedure, typically stochastic gradient descent or a modern variation, such as Adam. It may also require that you select any performance metrics to keep track of during the model training process.
From an API perspective, this involves calling a function to compile the model with the chosen configuration, which will prepare the appropriate data structures required for the efficient use of the model you have defined.
The optimizer can be specified as a string for a known optimizer class, e.g., ‘sgd‘ for stochastic gradient descent, or you can configure an instance of an optimizer class and use that.
For a list of supported optimizers, see this:
1
2
3
4
.
.
.
# compile the model
opt
=
SGD
(
learning_rate
=
0.01
,
momentum
=
0.9
)
model
.
compile
(
optimizer
=
opt
,
loss
=
‘binary_crossentropy’
)
The three most common loss functions are:
- ‘binary_crossentropy‘ for binary classification
- ‘sparse_categorical_crossentropy‘ for multi-class classification
- ‘mse‘ (mean squared error) for regression
1
2
3
.
.
.
# compile the model
model
.
compile
(
optimizer
=
‘sgd’
,
loss
=
‘mse’
)
For a list of supported loss functions, see:
Metrics are defined as a list of strings for known metric functions or a list of functions to call to evaluate predictions.
For a list of supported metrics, see:
1
2
3
.
.
.
# compile the model
model
.
compile
(
optimizer
=
‘sgd’
,
loss
=
‘binary_crossentropy’
,
metrics
=
[
‘accuracy’
]
)
Fit the Model
Fitting the model requires that you first select the training configuration, such as the number of epochs (loops through the training dataset) and the batch size (number of samples in an epoch used to estimate model error).
Training applies the chosen optimization algorithm to minimize the chosen loss function and updates the model using the backpropagation of the error algorithm.
Fitting the model is the slow part of the whole process and can take seconds to hours to days, depending on the complexity of the model, the hardware you’re using, and the size of the training dataset.
From an API perspective, this involves calling a function to perform the training process. This function will block (not return) until the training process has finished.
1
2
3
.
.
.
# fit the model
model
.
fit
(
X
,
y
,
epochs
=
100
,
batch_size
=
32
)
For help on how to choose the batch size, see this tutorial:
While fitting the model, a progress bar will summarize the status of each epoch and the overall training process. This can be simplified to a simple report of the model performance of each epoch by setting the “verbose” argument to 2. All output can be turned off during training by setting “verbose” to 0.
1
2
3
.
.
.
# fit the model
model
.
fit
(
X
,
y
,
epochs
=
100
,
batch_size
=
32
,
verbose
=
0
)
Evaluate the Model
Evaluating the model requires that you first choose a holdout dataset used to evaluate the model. This should be data not used in the training process so that you can get an unbiased estimate of the performance of the model when making predictions on new data.
The speed of a model evaluation is proportional to the amount of data you want to use for the evaluation, although it is much faster than training as the model is not changed.
From an API perspective, this involves calling a function with the holdout dataset and getting a loss and perhaps other metrics that can be reported.
1
2
3
.
.
.
# evaluate the model
loss
=
model
.
evaluate
(
X
,
y
,
verbose
=
0
)
Make a Prediction
Making a prediction is the final step in the life cycle. It is why we wanted the model in the first place.
It requires you have new data for which a prediction is required, e.g., where you do not have the target values.
From an API perspective, you simply call a function to make a prediction of a class label, probability, or numerical value—whatever you designed your model to predict.
You may want to save the model and later load it to make predictions. You may also choose to fit a model on all of the available data before you start using it.
Now that you are familiar with the model life-cycle let’s take a look at the two main ways to use the tf.keras API to build models: sequential and functional.
1
2
3
.
.
.
# make a prediction
yhat
=
model
.
predict
(
X
)
2.2 Sequential Model API (Simple)
The sequential model API is the simplest and the recommended API, especially when getting started.
It is referred to as “sequential” because it involves defining a Sequential class and adding layers to the model one by one in a linear manner, from input to output.
The example below defines a Sequential MLP model that accepts eight inputs, has one hidden layer with 10 nodes, and then an output layer with one node to predict a numerical value.
1
2
3
4
5
6
7
# example of a model defined with the sequential api
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
# define the model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
input_shape
=
(
8
,
)
)
)
model
.
add
(
Dense
(
1
)
)
Note that the visible layer of the network is defined by the “input_shape” argument on the first hidden layer. In the above example, the model expects the input for one sample to be a vector of eight numbers.
The sequential API is easy to use because you keep calling model.add() until you have added all your layers.
For example, here is a deep MLP with five hidden layers.
1
2
3
4
5
6
7
8
9
10
11
# example of a model defined with the sequential api
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
# define the model
model
=
Sequential
(
)
model
.
add
(
Dense
(
100
,
input_shape
=
(
8
,
)
)
)
model
.
add
(
Dense
(
80
)
)
model
.
add
(
Dense
(
30
)
)
model
.
add
(
Dense
(
10
)
)
model
.
add
(
Dense
(
5
)
)
model
.
add
(
Dense
(
1
)
)
2.3 Functional Model API (Advanced)
The functional API is more complex but is also more flexible.
It involves explicitly connecting the output of one layer to the input of another layer. Each connection is specified.
First, an input layer must be defined via the Input class, and the shape of an input sample is specified. We must retain a reference to the input layer when defining the model.
1
2
3
.
.
.
# define the layers
x_in
=
Input
(
shape
=
(
8
,
)
)
Next, a fully connected layer can be connected to the input by calling the layer and passing the input layer. This will return a reference to the output connection in this new layer.
1
2
.
.
.
x
=
Dense
(
10
)
(
x_in
)
We can then connect this to an output layer in the same manner.
1
2
.
.
.
x_out
=
Dense
(
1
)
(
x
)
Once connected, we define a Model object and specify the input and output layers. The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
# example of a model defined with the functional api
from
tensorflow
.
keras
import
Model
from
tensorflow
.
keras
import
Input
from
tensorflow
.
keras
.
layers
import
Dense
# define the layers
x_in
=
Input
(
shape
=
(
8
,
)
)
x
=
Dense
(
10
)
(
x_in
)
x_out
=
Dense
(
1
)
(
x
)
# define the model
model
=
Model
(
inputs
=
x_in
,
outputs
=
x_out
)
As such, it allows for more complicated model designs, such as models that may have multiple input paths (separate vectors) and models that have multiple output paths (e.g., a word and a number).
The functional API can be a lot of fun when you get used to it.
For more on the functional API, see:
Now that we are familiar with the model life cycle and the two APIs that can be used to define models, let’s look at developing some standard models.
3. How to Develop Deep Learning Models
In this section, you will discover how to develop, evaluate, and make predictions with standard deep learning models, including Multilayer Perceptrons (MLP), Convolutional Neural Networks (CNNs), and Recurrent Neural Networks (RNNs).
3.1 Develop Multilayer Perceptron Models
A Multilayer Perceptron model, or MLP for short, is a standard fully connected neural network model.
It comprises layers of nodes where each node is connected to all outputs from the previous layer, and the output of each node is connected to all inputs for nodes in the next layer.
An MLP is created with one or more Dense layers. This model is appropriate for tabular data, that is data as it looks in a table or spreadsheet with one column for each variable and one row for each variable. There are three predictive modeling problems you may want to explore with an MLP; they are binary classification, multiclass classification, and regression.
Let’s fit a model on a real dataset for each of these cases.
Note that the models in this section are effective but not optimized. See if you can improve their performance. Post your findings in the comments below.
MLP for Binary Classification
We will use the Ionosphere binary (two-class) classification dataset to demonstrate an MLP for binary classification.
This dataset involves predicting whether a structure is in the atmosphere or not, given radar returns.
The dataset will be downloaded automatically using Pandas, but you can learn more about it here.
We will use a LabelEncoder to encode the string labels to integer values 0 and 1. The model will be fit on 67% of the data, and the remaining 33% will be used for evaluation, split using the train_test_split() function.
It is good practice to use ‘relu‘ activation with a ‘he_normal‘ weight initialization. This combination goes a long way in overcoming the problem of vanishing gradients when training deep neural network models. For more on ReLU, see the tutorial:
The model predicts the probability of class 1 and uses the sigmoid activation function. The model is optimized using the adam version of stochastic gradient descent and seeks to minimize the cross-entropy loss.
The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# mlp for binary classification
from
pandas
import
read_csv
from
sklearn
.
model_selection
import
train_test_split
from
sklearn
.
preprocessing
import
LabelEncoder
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
# load the dataset
path
=
‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’
df
=
read_csv
(
path
,
header
=
None
)
# split into input and output columns
X
,
y
=
df
.
values
[
:
,
:
–
1
]
,
df
.
values
[
:
,
–
1
]
# ensure all data are floating point values
X
=
X
.
astype
(
‘float32’
)
# encode strings to integer
y
=
LabelEncoder
(
)
.
fit_transform
(
y
)
# split into train and test datasets
X_train
,
X_test
,
y_train
,
y_test
=
train_test_split
(
X
,
y
,
test_size
=
0.33
)
(
X_train
.
shape
,
X_test
.
shape
,
y_train
.
shape
,
y_test
.
shape
)
# determine the number of input features
n_features
=
X_train
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
Dense
(
8
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# compile the model
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘binary_crossentropy’
,
metrics
=
[
‘accuracy’
]
)
# fit the model
model
.
fit
(
X_train
,
y_train
,
epochs
=
150
,
batch_size
=
32
,
verbose
=
0
)
# evaluate the model
loss
,
acc
=
model
.
evaluate
(
X_test
,
y_test
,
verbose
=
0
)
(
‘Test Accuracy: %.3f’
%
acc
)
# make a prediction
row
=
[
1
,
0
,
0.99539
,
–
0.05889
,
0.85243
,
0.02306
,
0.83398
,
–
0.37708
,
1
,
0.03760
,
0.85243
,
–
0.17755
,
0.59755
,
–
0.44945
,
0.60536
,
–
0.38223
,
0.84356
,
–
0.38542
,
0.58212
,
–
0.32192
,
0.56971
,
–
0.29674
,
0.36946
,
–
0.47357
,
0.56811
,
–
0.51171
,
0.41078
,
–
0.46168
,
0.21266
,
–
0.34090
,
0.42267
,
–
0.54487
,
0.18641
,
–
0.45300
]
yhat
=
model
.
predict
(
[
row
]
)
(
‘Predicted: %.3f’
%
yhat
)
Running the example first reports the shape of the dataset then fits the model and evaluates it on the test dataset. Finally, a prediction is made for a single row of data.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
What results did you get? Can you change the model to do better?
Post your findings in the comments below.
In this case, we can see that the model achieved a classification accuracy of about 94% and then predicted a probability of 0.9 that the one row of data belongs to class 1.
1
2
3
(235, 34) (116, 34) (235,) (116,)
Test Accuracy: 0.940
Predicted: 0.991
MLP for Multiclass Classification
We will use the Iris flowers multiclass classification dataset to demonstrate an MLP for multiclass classification.
This problem involves predicting the species of iris flower given measures of the flower.
The dataset will be downloaded automatically using Pandas, but you can learn more about it here.
Given that it is a multiclass classification, the model must have one node for each class in the output layer and use the softmax activation function. The loss function is the ‘sparse_categorical_crossentropy‘, which is appropriate for integer encoded class labels (e.g., 0 for one class, 1 for the next class, etc.)
The complete example of fitting and evaluating an MLP on the iris flowers dataset is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# mlp for multiclass classification
from
numpy
import
argmax
from
pandas
import
read_csv
from
sklearn
.
model_selection
import
train_test_split
from
sklearn
.
preprocessing
import
LabelEncoder
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
# load the dataset
path
=
‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/iris.csv’
df
=
read_csv
(
path
,
header
=
None
)
# split into input and output columns
X
,
y
=
df
.
values
[
:
,
:
–
1
]
,
df
.
values
[
:
,
–
1
]
# ensure all data are floating point values
X
=
X
.
astype
(
‘float32’
)
# encode strings to integer
y
=
LabelEncoder
(
)
.
fit_transform
(
y
)
# split into train and test datasets
X_train
,
X_test
,
y_train
,
y_test
=
train_test_split
(
X
,
y
,
test_size
=
0.33
)
(
X_train
.
shape
,
X_test
.
shape
,
y_train
.
shape
,
y_test
.
shape
)
# determine the number of input features
n_features
=
X_train
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
Dense
(
8
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
)
)
model
.
add
(
Dense
(
3
,
activation
=
‘softmax’
)
)
# compile the model
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘sparse_categorical_crossentropy’
,
metrics
=
[
‘accuracy’
]
)
# fit the model
model
.
fit
(
X_train
,
y_train
,
epochs
=
150
,
batch_size
=
32
,
verbose
=
0
)
# evaluate the model
loss
,
acc
=
model
.
evaluate
(
X_test
,
y_test
,
verbose
=
0
)
(
‘Test Accuracy: %.3f’
%
acc
)
# make a prediction
row
=
[
5.1
,
3.5
,
1.4
,
0.2
]
yhat
=
model
.
predict
(
[
row
]
)
(
‘Predicted: %s (class=%d)’
%
(
yhat
,
argmax
(
yhat
)
)
)
Running the example first reports the shape of the dataset then fits the model and evaluates it on the test dataset. Finally, a prediction is made for a single row of data.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
What results did you get? Can you change the model to do better?
Post your findings in the comments below.
In this case, we can see that the model achieved a classification accuracy of about 98% and then predicted a probability of a row of data belonging to each class, although class 0 has the highest probability.
1
2
3
(100, 4) (50, 4) (100,) (50,)
Test Accuracy: 0.980
Predicted: [[0.8680804 0.12356871 0.00835086]] (class=0)
MLP for Regression
We will use the Boston housing regression dataset to demonstrate an MLP for regression predictive modeling.
This problem involves predicting house value based on the properties of the house and neighborhood.
The dataset will be downloaded automatically using Pandas, but you can learn more about it here.
This is a regression problem that involves predicting a single numerical value. As such, the output layer has a single node and uses the default or linear activation function (no activation function). The mean squared error (mse) loss is minimized when fitting the model.
Recall that this is a regression, not a classification; therefore, we cannot calculate classification accuracy. For more on this, see the tutorial:
The complete example of fitting and evaluating an MLP on the Boston housing dataset is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# mlp for regression
from
numpy
import
sqrt
from
pandas
import
read_csv
from
sklearn
.
model_selection
import
train_test_split
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
# load the dataset
path
=
‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv’
df
=
read_csv
(
path
,
header
=
None
)
# split into input and output columns
X
,
y
=
df
.
values
[
:
,
:
–
1
]
,
df
.
values
[
:
,
–
1
]
# split into train and test datasets
X_train
,
X_test
,
y_train
,
y_test
=
train_test_split
(
X
,
y
,
test_size
=
0.33
)
(
X_train
.
shape
,
X_test
.
shape
,
y_train
.
shape
,
y_test
.
shape
)
# determine the number of input features
n_features
=
X_train
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
Dense
(
8
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
)
)
model
.
add
(
Dense
(
1
)
)
# compile the model
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘mse’
)
# fit the model
model
.
fit
(
X_train
,
y_train
,
epochs
=
150
,
batch_size
=
32
,
verbose
=
0
)
# evaluate the model
error
=
model
.
evaluate
(
X_test
,
y_test
,
verbose
=
0
)
(
‘MSE: %.3f, RMSE: %.3f’
%
(
error
,
sqrt
(
error
)
)
)
# make a prediction
row
=
[
0.00632
,
18.00
,
2.310
,
0
,
0.5380
,
6.5750
,
65.20
,
4.0900
,
1
,
296.0
,
15.30
,
396.90
,
4.98
]
yhat
=
model
.
predict
(
[
row
]
)
(
‘Predicted: %.3f’
%
yhat
)
Running the example first reports the shape of the dataset then fits the model and evaluates it on the test dataset. Finally, a prediction is made for a single row of data.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
What results did you get? Can you change the model to do better?
Post your findings in the comments below.
In this case, we can see that the model achieved an MSE of about 60, which is an RMSE of about 7 (units are thousands of dollars). A value of about 26 is then predicted for the single example.
1
2
3
(339, 13) (167, 13) (339,) (167,)
MSE: 60.751, RMSE: 7.794
Predicted: 26.983
3.2 Develop Convolutional Neural Network Models
Convolutional Neural Networks, or CNNs for short, are a type of network designed for image input.
They are comprised of models with convolutional layers that extract features (called feature maps) and pooling layers that distill features down to the most salient elements.
CNNs are most well-suited to image classification tasks, although they can be used on a wide array of tasks that take images as input.
A popular image classification task is the MNIST handwritten digit classification. It involves tens of thousands of handwritten digits that must be classified as a number between 0 and 9.
The tf.keras API provides a convenient function to download and load this dataset directly.
The example below loads the dataset and plots the first few images.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# example of loading and plotting the mnist dataset
from
tensorflow
.
keras
.
datasets
.
mnist
import
load_data
from
matplotlib
import
pyplot
# load dataset
(
trainX
,
trainy
)
,
(
testX
,
testy
)
=
load_data
(
)
# summarize loaded dataset
(
‘Train: X=%s, y=%s’
%
(
trainX
.
shape
,
trainy
.
shape
)
)
(
‘Test: X=%s, y=%s’
%
(
testX
.
shape
,
testy
.
shape
)
)
# plot first few images
for
i
in
range
(
25
)
:
# define subplot
pyplot
.
subplot
(
5
,
5
,
i
+
1
)
# plot raw pixel data
pyplot
.
imshow
(
trainX
[
i
]
,
cmap
=
pyplot
.
get_cmap
(
‘gray’
)
)
# show the figure
pyplot
.
show
(
)
Running the example loads the MNIST dataset, then summarizes the default train and test datasets.
1
2
Train: X=(60000, 28, 28), y=(60000,)
Test: X=(10000, 28, 28), y=(10000,)
A plot is then created showing a grid of examples of handwritten images in the training dataset.

We can train a CNN model to classify the images in the MNIST dataset.
Note that the images are arrays of grayscale pixel data; therefore, we must add a channel dimension to the data before we can use the images as input to the model. The reason is that CNN models expect images in a channels-last format; that is, each example to the network has the dimensions [rows, columns, channels], where channels represent the color channels of the image data.
It is also a good idea to scale the pixel values from the default range of 0-255 to 0-1 when training a CNN. For more on scaling pixel values, see the tutorial:
The complete example of fitting and evaluating a CNN model on the MNIST dataset is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# example of a cnn for image classification
from
numpy
import
asarray
from
numpy
import
unique
from
numpy
import
argmax
from
tensorflow
.
keras
.
datasets
.
mnist
import
load_data
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
layers
import
Conv2D
from
tensorflow
.
keras
.
layers
import
MaxPool2D
from
tensorflow
.
keras
.
layers
import
Flatten
from
tensorflow
.
keras
.
layers
import
Dropout
# load dataset
(
x_train
,
y_train
)
,
(
x_test
,
y_test
)
=
load_data
(
)
# reshape data to have a single channel
x_train
=
x_train
.
reshape
(
(
x_train
.
shape
[
0
]
,
x_train
.
shape
[
1
]
,
x_train
.
shape
[
2
]
,
1
)
)
x_test
=
x_test
.
reshape
(
(
x_test
.
shape
[
0
]
,
x_test
.
shape
[
1
]
,
x_test
.
shape
[
2
]
,
1
)
)
# determine the shape of the input images
in_shape
=
x_train
.
shape
[
1
:
]
# determine the number of classes
n_classes
=
len
(
unique
(
y_train
)
)
(
in_shape
,
n_classes
)
# normalize pixel values
x_train
=
x_train
.
astype
(
‘float32’
)
/
255.0
x_test
=
x_test
.
astype
(
‘float32’
)
/
255.0
# define model
model
=
Sequential
(
)
model
.
add
(
Conv2D
(
32
,
(
3
,
3
)
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_uniform’
,
input_shape
=
in_shape
)
)
model
.
add
(
MaxPool2D
(
(
2
,
2
)
)
)
model
.
add
(
Flatten
(
)
)
model
.
add
(
Dense
(
100
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_uniform’
)
)
model
.
add
(
Dropout
(
0.5
)
)
model
.
add
(
Dense
(
n_classes
,
activation
=
‘softmax’
)
)
# define loss and optimizer
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘sparse_categorical_crossentropy’
,
metrics
=
[
‘accuracy’
]
)
# fit the model
model
.
fit
(
x_train
,
y_train
,
epochs
=
10
,
batch_size
=
128
,
verbose
=
0
)
# evaluate the model
loss
,
acc
=
model
.
evaluate
(
x_test
,
y_test
,
verbose
=
0
)
(
‘Accuracy: %.3f’
%
acc
)
# make a prediction
image
=
x_train
[
0
]
yhat
=
model
.
predict
(
asarray
(
[
image
]
)
)
(
‘Predicted: class=%d’
%
argmax
(
yhat
)
)
Running the example first reports the shape of the dataset then fits the model and evaluates it on the test dataset. Finally, a prediction is made for a single image.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
What results did you get? Can you change the model to do better?
Post your findings in the comments below.
First, the shape of each image is reported along with the number of classes; we can see that each image is 28×28 pixels, and there are 10 classes, as we expected.
In this case, we can see that the model achieved a classification accuracy of about 98% on the test dataset. We can then see that the model predicted class 5 for the first image in the training set.
1
2
3
(28, 28, 1) 10
Accuracy: 0.987
Predicted: class=5
3.3 Develop Recurrent Neural Network Models
Recurrent Neural Networks, or RNNs for short, are designed to operate upon sequences of data.
They have proven to be very effective for natural language processing problems where sequences of text are provided as input to the model. RNNs have also seen some modest success in time series forecasting and speech recognition.
The most popular type of RNN is the Long Short-Term Memory network or LSTM for short. LSTMs can be used in a model to accept a sequence of input data and make a prediction, such as assign a class label or predict a numerical value like the next value or values in the sequence.
You will use the car sales dataset to demonstrate an LSTM RNN for univariate time series forecasting.
This problem involves predicting the number of car sales per month.
The dataset will be downloaded automatically using Pandas, but you can learn more about it here.
Let’s frame the problem to take a window of the last five months of data to predict the current month’s data.
To achieve this, you define a new function named split_sequence() that will split the input sequence into windows of data appropriate for fitting a supervised learning model, like an LSTM.
For example, if the sequence was:
1
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Then the samples for training the model would look like:
1
2
3
4
5
Input Output
1, 2, 3, 4, 5 6
2, 3, 4, 5, 6 7
3, 4, 5, 6, 7 8
…
Use the last 12 months of data as the test dataset.
LSTMs expect each sample in the dataset to have two dimensions; the first is the number of time steps (in this case, it is 5), and the second is the number of observations per time step (in this case, it is 1).
Because it is a regression-type problem, we will use a linear activation function (no activation function) in the output layer and optimize the mean squared error loss function. We will also evaluate the model using the mean absolute error (MAE) metric.
The complete example of fitting and evaluating an LSTM for a univariate time series forecasting problem is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# lstm for time series forecasting
from
numpy
import
sqrt
from
numpy
import
asarray
from
pandas
import
read_csv
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
layers
import
LSTM
# split a univariate sequence into samples
def
split_sequence
(
sequence
,
n_steps
)
:
X
,
y
=
list
(
)
,
list
(
)
for
i
in
range
(
len
(
sequence
)
)
:
# find the end of this pattern
end_ix
=
i
+
n
_
steps
# check if we are beyond the sequence
if
end_ix
>
len
(
sequence
)
–
1
:
break
# gather input and output parts of the pattern
seq_x
,
seq_y
=
sequence
[
i
:
end_ix
]
,
sequence
[
end_ix
]
X
.
append
(
seq_x
)
y
.
append
(
seq_y
)
return
asarray
(
X
)
,
asarray
(
y
)
# load the dataset
path
=
‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-car-sales.csv’
df
=
read_csv
(
path
,
header
=
0
,
index_col
=
0
,
squeeze
=
True
)
# retrieve the values
values
=
df
.
values
.
astype
(
‘float32’
)
# specify the window size
n_steps
=
5
# split into samples
X
,
y
=
split_sequence
(
values
,
n_steps
)
# reshape into [samples, timesteps, features]
X
=
X
.
reshape
(
(
X
.
shape
[
0
]
,
X
.
shape
[
1
]
,
1
)
)
# split into train/test
n_test
=
12
X_train
,
X_test
,
y_train
,
y_test
=
X
[
:
–
n_test
]
,
X
[
–
n_test
:
]
,
y
[
:
–
n_test
]
,
y
[
–
n_test
:
]
(
X_train
.
shape
,
X_test
.
shape
,
y_train
.
shape
,
y_test
.
shape
)
# define model
model
=
Sequential
(
)
model
.
add
(
LSTM
(
100
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_steps
,
1
)
)
)
model
.
add
(
Dense
(
50
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
)
)
model
.
add
(
Dense
(
50
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
)
)
model
.
add
(
Dense
(
1
)
)
# compile the model
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘mse’
,
metrics
=
[
‘mae’
]
)
# fit the model
model
.
fit
(
X_train
,
y_train
,
epochs
=
350
,
batch_size
=
32
,
verbose
=
2
,
validation_data
=
(
X_test
,
y_test
)
)
# evaluate the model
mse
,
mae
=
model
.
evaluate
(
X_test
,
y_test
,
verbose
=
0
)
(
‘MSE: %.3f, RMSE: %.3f, MAE: %.3f’
%
(
mse
,
sqrt
(
mse
)
,
mae
)
)
# make a prediction
row
=
asarray
(
[
18024.0
,
16722.0
,
14385.0
,
21342.0
,
17180.0
]
)
.
reshape
(
(
1
,
n_steps
,
1
)
)
yhat
=
model
.
predict
(
row
)
(
‘Predicted: %.3f’
%
(
yhat
)
)
Running the example first reports the shape of the dataset then fits the model and evaluates it on the test dataset. Finally, a prediction is made for a single example.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
What results did you get? Can you change the model to do better?
Post your findings in the comments below.
First, the shape of the train and test datasets is displayed, confirming that the last 12 examples are used for model evaluation.
In this case, the model achieved an MAE of about 2,800 and predicted the next value in the sequence from the test set as 13,199, where the expected value is 14,577 (pretty close).
1
2
3
(91, 5, 1) (12, 5, 1) (91,) (12,)
MSE: 12755421.000, RMSE: 3571.473, MAE: 2856.084
Predicted: 13199.325
Note: it is good practice to scale and make the series stationary data prior to fitting the model. I recommend this as an extension to achieve better performance. For more on preparing time series data for modeling, see the tutorial:
4. How to Use Advanced Model Features
In this section, you will discover how to use some of the slightly more advanced model features, such as reviewing learning curves and saving models for later use.
4.1 How to Visualize a Deep Learning Model
The architecture of deep learning models can quickly become large and complex.
As such, it is important to have a clear idea of the connections and data flow in your model. This is especially important if you are using the functional API to ensure you have indeed connected the layers of the model in the way you intended.
There are two tools you can use to visualize your model: a text description and a plot.
Model Text Description
A text description of your model can be displayed by calling the summary() function on your model.
The example below defines a small model with three layers and then summarizes the structure.
1
2
3
4
5
6
7
8
9
10
# example of summarizing a model
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
8
,
)
)
)
model
.
add
(
Dense
(
8
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# summarize the model
model
.
summary
(
)
Running the example prints a summary of each layer and a total summary.
This is an invaluable diagnostic for checking the output shapes and the number of parameters (weights) in your model.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Model: “sequential”
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 10) 90
_________________________________________________________________
dense_1 (Dense) (None, 8) 88
_________________________________________________________________
dense_2 (Dense) (None, 1) 9
=================================================================
Total params: 187
Trainable params: 187
Non-trainable params: 0
_________________________________________________________________
Model Architecture Plot
You can create a plot of your model by calling the plot_model() function.
This will create an image file that contains a box and line diagram of the layers in your model.
The example below creates a small three-layer model and saves a plot of the model architecture to ‘model.png‘ that includes input and output shapes.
1
2
3
4
5
6
7
8
9
10
11
# example of plotting a model
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
utils
import
plot
_
model
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
8
,
)
)
)
model
.
add
(
Dense
(
8
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# summarize the model
plot_model
(
model
,
‘model.png’
,
show_shapes
=
True
)
Running the example creates a plot of the model showing a box for each layer with shape information and arrows that connect the layers, showing the flow of data through the network.
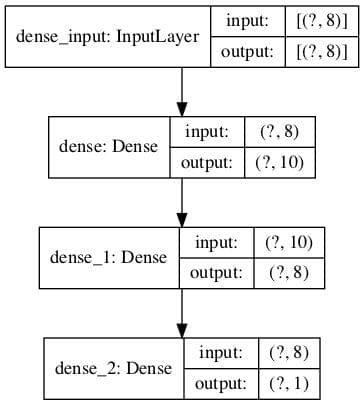
4.2 How to Plot Model Learning Curves
Learning curves are a plot of neural network model performance over time, such as those calculated at the end of each training epoch.
Plots of learning curves provide insight into the learning dynamics of the model, such as whether the model is learning well, underfitting the training dataset, or overfitting the training dataset.
For a gentle introduction to learning curves and how to use them to diagnose the learning dynamics of models, see the tutorial:
You can easily create learning curves for your deep learning models.
First, you must update your call to the fit function to include a reference to a validation dataset. This is a portion of the training set not used to fit the model and is instead used to evaluate the performance of the model during training.
You can split the data manually and specify the validation_data argument, or you can use the validation_split argument and specify a percentage split of the training dataset and let the API perform the split for you. The latter is simpler for now.
The fit function will return a history object that contains a trace of performance metrics recorded at the end of each training epoch. This includes the chosen loss function and each configured metric, such as accuracy, and each loss and metric is calculated for the training and validation datasets.
A learning curve is a plot of the loss on the training dataset and the validation dataset. We can create this plot from the history object using the Matplotlib library.
The example below fits a small neural network on a synthetic binary classification problem. A validation split of 30% is used to evaluate the model during training, and the cross-entropy loss on the train and validation datasets are then graphed using a line plot.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# example of plotting learning curves
from
sklearn
.
datasets
import
make_classification
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
optimizers
import
SGD
from
matplotlib
import
pyplot
# create the dataset
X
,
y
=
make_classification
(
n_samples
=
1000
,
n_classes
=
2
,
random_state
=
1
)
# determine the number of input features
n_features
=
X
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# compile the model
sgd
=
SGD
(
learning_rate
=
0.001
,
momentum
=
0.8
)
model
.
compile
(
optimizer
=
sgd
,
loss
=
‘binary_crossentropy’
)
# fit the model
history
=
model
.
fit
(
X
,
y
,
epochs
=
100
,
batch_size
=
32
,
verbose
=
0
,
validation_split
=
0.3
)
# plot learning curves
pyplot
.
title
(
‘Learning Curves’
)
pyplot
.
xlabel
(
‘Epoch’
)
pyplot
.
ylabel
(
‘Cross Entropy’
)
pyplot
.
plot
(
history
.
history
[
‘loss’
]
,
label
=
‘train’
)
pyplot
.
plot
(
history
.
history
[
‘val_loss’
]
,
label
=
‘val’
)
pyplot
.
legend
(
)
pyplot
.
show
(
)
Running the example fits the model on the dataset. At the end of the run, the history object is returned and used as the basis for creating the line plot.
The cross-entropy loss for the training dataset is accessed via the ‘loss‘ key, and the loss on the validation dataset is accessed via the ‘val_loss‘ key on the history attribute of the history object.
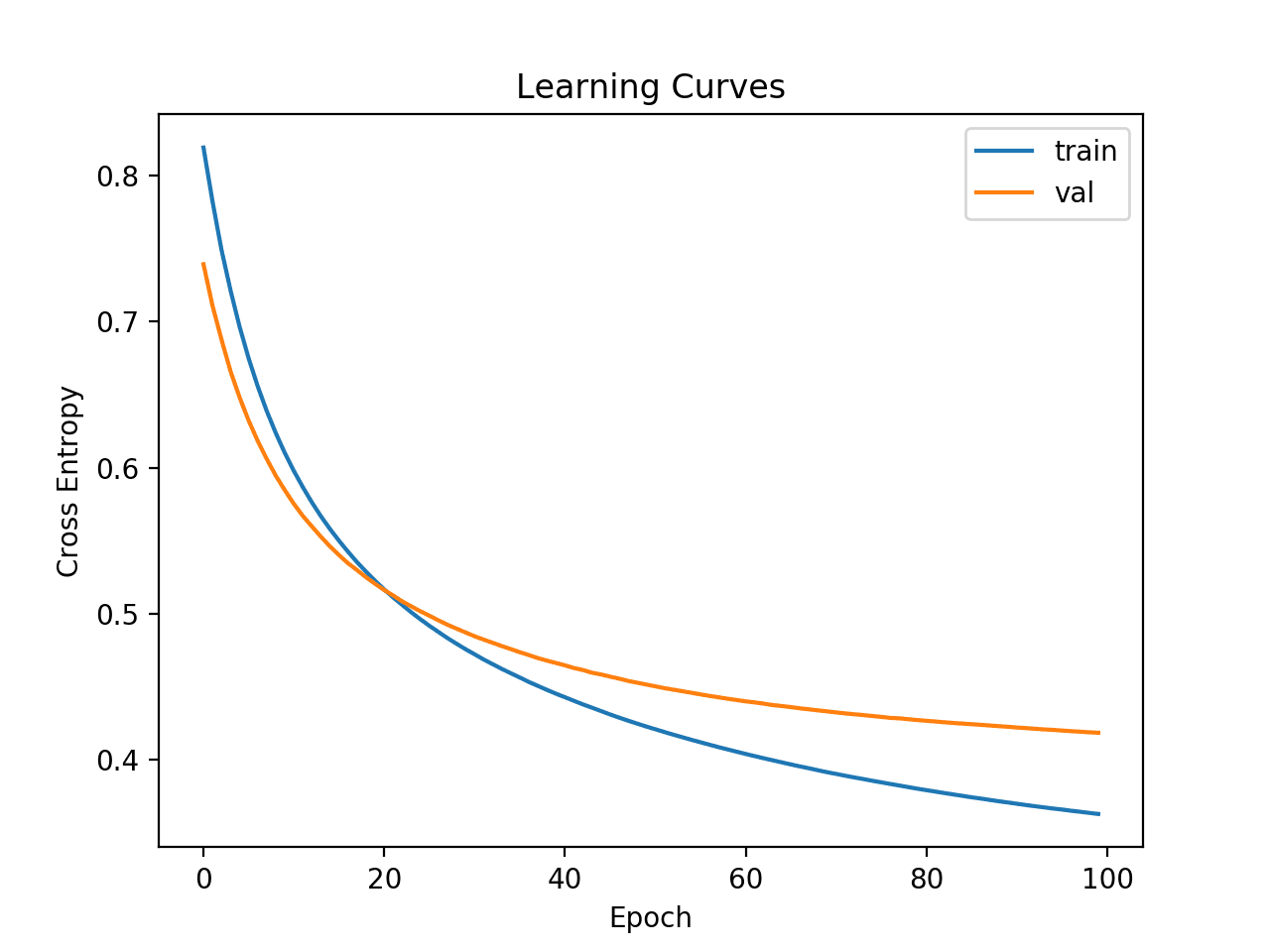
4.3 How to Save and Load Your Model
Training and evaluating models is great, but we may want to use a model later without retraining it each time.
This can be achieved by saving the model to a file, loading it later, and using it to make predictions.
This can be achieved using the save() function on the model to save the model. It can be loaded later using the load_model() function.
The model is saved in H5 format, an efficient array storage format. As such, you must ensure that the h5py library is installed on your workstation. This can be achieved using pip, for example:
1
pip install h5py
The example below fits a simple model on a synthetic binary classification problem and then saves the model file.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# example of saving a fit model
from
sklearn
.
datasets
import
make_classification
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
optimizers
import
SGD
# create the dataset
X
,
y
=
make_classification
(
n_samples
=
1000
,
n_features
=
4
,
n_classes
=
2
,
random_state
=
1
)
# determine the number of input features
n_features
=
X
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# compile the model
sgd
=
SGD
(
learning_rate
=
0.001
,
momentum
=
0.8
)
model
.
compile
(
optimizer
=
sgd
,
loss
=
‘binary_crossentropy’
)
# fit the model
model
.
fit
(
X
,
y
,
epochs
=
100
,
batch_size
=
32
,
verbose
=
0
,
validation_split
=
0.3
)
# save model to file
model
.
save
(
‘model.h5’
)
Running the example fits the model and saves it to a file with the name ‘model.h5‘.
You can then load the model and use it to make a prediction, continue training it, or do whatever you wish with it.
The example below loads the model and uses it to make a prediction.
1
2
3
4
5
6
7
8
9
10
11
# example of loading a saved model
from
sklearn
.
datasets
import
make_classification
from
tensorflow
.
keras
.
models
import
load
_
model
# create the dataset
X
,
y
=
make_classification
(
n_samples
=
1000
,
n_features
=
4
,
n_classes
=
2
,
random_state
=
1
)
# load the model from file
model
=
load_model
(
‘model.h5’
)
# make a prediction
row
=
[
1.91518414
,
1.14995454
,
–
1.52847073
,
0.79430654
]
yhat
=
model
.
predict
(
[
row
]
)
(
‘Predicted: %.3f’
%
yhat
[
0
]
)
Running the example loads the image from the file, then uses it to make a prediction on a new row of data and prints the result.
1
Predicted: 0.831
5. How to Get Better Model Performance
In this section, you will discover some of the techniques that you can use to improve the performance of your deep learning models.
A big part of improving deep learning performance involves avoiding overfitting by slowing down the learning process or stopping the learning process at the right time.
5.1 How to Reduce Overfitting with Dropout
Dropout is a clever regularization method that reduces the overfitting of the training dataset and makes the model more robust.
This is achieved during training, where some number of layer outputs are randomly ignored or “dropped out.” This has the effect of making the layer look like—and be treated like—a layer with a different number of nodes and connectivity to the prior layer.
Dropout has the effect of making the training process noisy, forcing nodes within a layer to take on more or less responsibility for the inputs probabilistically.
For more on how dropout works, see this tutorial:
You can add dropout to your models as a new layer prior to the layer that you want to have input connections dropped out.
This involves adding a layer called Dropout() that takes an argument specifying the probability that each output from the previous will drop, e.g., 0.4 means 40% percent of inputs will be dropped each update to the model.
You can add Dropout layers in MLP, CNN, and RNN models, although there are also specialized versions of dropout for use with CNN and RNN models that you might also want to explore.
The example below fits a small neural network model on a synthetic binary classification problem.
A dropout layer with 50% dropout is inserted between the first hidden layer and the output layer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# example of using dropout
from
sklearn
.
datasets
import
make_classification
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
layers
import
Dropout
from
matplotlib
import
pyplot
# create the dataset
X
,
y
=
make_classification
(
n_samples
=
1000
,
n_classes
=
2
,
random_state
=
1
)
# determine the number of input features
n_features
=
X
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
Dropout
(
0.5
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# compile the model
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘binary_crossentropy’
)
# fit the model
model
.
fit
(
X
,
y
,
epochs
=
100
,
batch_size
=
32
,
verbose
=
0
)
5.2 How to Accelerate Training with Batch Normalization
The scale and distribution of inputs to a layer can greatly impact how easy or quickly that layer can be trained.
This is generally why it is a good idea to scale input data prior to modeling it with a neural network model.
Batch normalization is a technique for training very deep neural networks that standardizes the inputs to a layer for each mini-batch. This has the effect of stabilizing the learning process and dramatically reducing the number of training epochs required to train deep networks.
For more on how batch normalization works, see this tutorial:
You can use batch normalization in your network by adding a batch normalization layer prior to the layer that you wish to have standardized inputs. You can use batch normalization with MLP, CNN, and RNN models.
This can be achieved by adding the BatchNormalization layer directly.
The example below defines a small MLP network for a binary classification prediction problem with a batch normalization layer between the first hidden layer and the output layer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# example of using batch normalization
from
sklearn
.
datasets
import
make_classification
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
layers
import
BatchNormalization
from
matplotlib
import
pyplot
# create the dataset
X
,
y
=
make_classification
(
n_samples
=
1000
,
n_classes
=
2
,
random_state
=
1
)
# determine the number of input features
n_features
=
X
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
BatchNormalization
(
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# compile the model
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘binary_crossentropy’
)
# fit the model
model
.
fit
(
X
,
y
,
epochs
=
100
,
batch_size
=
32
,
verbose
=
0
)
Also, tf.keras has a range of other normalization layers you might like to explore; see:
5.3 How to Halt Training at the Right Time with Early Stopping
Neural networks are challenging to train.
Too little training and the model is underfit; too much training and the model overfits the training dataset. Both cases result in a model that is less effective than it could be.
One approach to solving this problem is to use early stopping. This involves monitoring the loss on the training dataset and a validation dataset (a subset of the training set not used to fit the model). As soon as loss for the validation set starts to show signs of overfitting, the training process can be stopped.
For more on early stopping, see the tutorial:
Early stopping can be used with your model by first ensuring that you have a validation dataset. You can define the validation dataset manually via the validation_data argument to the fit() function, or you can use the validation_split and specify the amount of the training dataset to hold back for validation.
You can then define an EarlyStopping and instruct it on which performance measure to monitor, such as ‘val_loss‘ for loss on the validation dataset and the number of epochs to observe overfitting before taking action, e.g., 5.
This configured EarlyStopping callback can then be provided to the fit() function via the “callbacks” argument that takes a list of callbacks.
This allows you to set the number of epochs to a large number and be confident that training will end as soon as the model starts overfitting. You might also want to create a learning curve to discover more insights into the learning dynamics of the run and when training was halted.
The example below demonstrates a small neural network on a synthetic binary classification problem that uses early stopping to halt training as soon as the model starts overfitting (after about 50 epochs).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# example of using early stopping
from
sklearn
.
datasets
import
make_classification
from
tensorflow
.
keras
import
Sequential
from
tensorflow
.
keras
.
layers
import
Dense
from
tensorflow
.
keras
.
callbacks
import
EarlyStopping
# create the dataset
X
,
y
=
make_classification
(
n_samples
=
1000
,
n_classes
=
2
,
random_state
=
1
)
# determine the number of input features
n_features
=
X
.
shape
[
1
]
# define model
model
=
Sequential
(
)
model
.
add
(
Dense
(
10
,
activation
=
‘relu’
,
kernel_initializer
=
‘he_normal’
,
input_shape
=
(
n_features
,
)
)
)
model
.
add
(
Dense
(
1
,
activation
=
‘sigmoid’
)
)
# compile the model
model
.
compile
(
optimizer
=
‘adam’
,
loss
=
‘binary_crossentropy’
)
# configure early stopping
es
=
EarlyStopping
(
monitor
=
‘val_loss’
,
patience
=
5
)
# fit the model
history
=
model
.
fit
(
X
,
y
,
epochs
=
200
,
batch_size
=
32
,
verbose
=
0
,
validation_split
=
0.3
,
callbacks
=
[
es
]
)
The tf.keras API provides a number of callbacks that you might like to explore; you can learn more here:
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
Books
Guides
APIs
Summary
In this tutorial, you discovered a step-by-step guide to developing deep learning models in TensorFlow using the tf.keras API.
Specifically, you learned:
- The difference between Keras and tf.keras and how to install and confirm TensorFlow is working
- The 5-step life cycle of tf.keras models and how to use the sequential and functional APIs
- How to develop MLP, CNN, and RNN models with tf.keras for regression, classification, and time series forecasting
- How to use the advanced features of the tf.keras API to inspect and diagnose your model
- How to improve the performance of your tf.keras model by reducing overfitting and accelerating training
Do you have any questions?
Ask your questions in the comments below, and I will do my best to answer.















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


