Mạng lưới Bayesian – tìm hiểu và ứng dụng trong R – w3seo

Rate this post

Động cơ chính của hướng dẫn này là cung cấp cho bạn mô tả chi tiết về Mạng Bayes. Chúng tôi cũng sẽ trình bày ví dụ về Mạng Bayes và các đặc điểm khác nhau của nó trong lập trình R.

Các bài viết liên quan:

Bayesian Networks trong R cung cấp mô hình hoàn chỉnh của các biến và các mối quan hệ liên quan của chúng. Chúng tôi sử dụng chúng để trả lời các truy vấn xác suất.

Vì vậy, chúng ta hãy bắt đầu hướng dẫn.

Thống kê Bayes là gì?

Định lý Bayes là cơ sở của thống kê Bayes. Nó cho phép người dùng cập nhật xác suất của các sự kiện không được quan sát. Hãy xem xét rằng bạn có xác suất trước cho sự kiện không được quan sát và một sự kiện liên quan đã xảy ra. Bây giờ bạn có thể cập nhật xác suất trước để lấy xác suất sau của sự kiện.

Định lý Bayes tìm mật độ sau của các tham số cho một dữ liệu nhất định. Nó kết hợp thông tin về các tham số từ mật độ trước với dữ liệu quan sát.

Định lý Bayes – Đó là một lý thuyết xác suất được phát biểu bởi Mục sư Thomas Bayes. Một phần bằng chứng mới ảnh hưởng đến cách hiểu lý thuyết xác suất đúng như thế nào. Chúng tôi sử dụng nó trong nhiều bối cảnh khác nhau, từ sinh vật biển đến việc phát triển trình chặn thư rác “Bayesian” cho hệ thống email.

Khi được áp dụng, các xác suất liên quan đến định lý Bayes có thể có một số cách giải thích xác suất. Có việc sử dụng định lý như một phần của một cách tiếp cận cụ thể đối với suy luận thống kê.

Mạng Bayes là gì?

Mạng Bayes (BN) là một đồ thị chu kỳ được đánh dấu. Nó đại diện cho một JPD qua một tập hợp các ngẫu nhiên các biến V .

Bằng cách sử dụng mô hình đồ họa có hướng, Bayesian Network mô tả các biến ngẫu nhiên và các phụ thuộc có điều kiện. Ví dụ: bạn có thể sử dụng BN cho một bệnh nhân mắc một bệnh cụ thể. Bằng cách kiểm tra các yếu tố sức khỏe khác nhau, chúng tôi sử dụng BN để tính xác suất của các bệnh liên quan khác. Một số ví dụ là mạng cây thông thường gen, cấu trúc protein, phân tích biểu hiện gen.  Phương trình sau đây xác định nó:

B = (G, Θ)

Nơi đây:

• B là Mạng Bayes.
• G là Đồ thị vòng có hướng (DAG). Các nút X1, X2,… Xn của nó đại diện cho các biến ngẫu nhiên. Các cạnh của nó đại diện cho sự phụ thuộc trực tiếp giữa các biến này. Nó mã hóa các giả định về tính độc lập theo đó mỗi biến Xi độc lập với các biến không phải là hậu duệ của nó do cha mẹ của nó ở G.
• Θ đại diện cho tập hợp các tham số BN. Tập hợp này chứa tham số Θxi | πi = PB (xi | πi cho mỗi lần thực của xi được điều kiện hóa trên π ©, tập bố mẹ của Xi trong G.

B là Bayesian Network xác định một JPD duy nhất trên V, như sau:

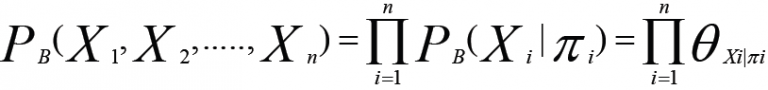
Trong phương trình trên, đối với các biến ngẫu nhiên xi có cha mẹ, phân phối xác suất cục bộ của chúng là có điều kiện. Phân phối xác suất cho các biến khác là vô điều kiện. Các nút bằng chứng là các nút đại diện cho một biến quan sát được trong khi các nút không nhìn thấy hoặc ẩn là các nút đại diện cho các biến không thể quan sát được. Đối với một BN, bạn phải chỉ định cấu trúc và các tham số cho mô hình đồ thị.

Phân phối xác suất có điều kiện (CPD) xác định các tham số tại mỗi nút và  Bảng xác suất có điều kiện (CPT) xác định CDP trong các biến rời rạc. Sử dụng kết hợp các giá trị khác nhau từ cha mẹ, CPT đại diện cho xác suất của một nút con.

Mạng Bayes là một mô hình hoàn chỉnh cho các biến và mối quan hệ của chúng. Chúng tôi sử dụng nó để trả lời các truy vấn xác suất về chúng.

Ví dụ về Mạng Bayes trong R

Giả sử bạn muốn xác định khả năng cỏ bị ướt hoặc khô do sự xuất hiện của các mùa khác nhau.

Thời tiết có ba trạng thái: Nắng, Nhiều mây và Mưa . Có hai khả năng cho cỏ: Ướt hoặc khô.

Vòi phun nước có thể bật hoặc tắt. Nếu trời mưa, cỏ bị ướt nhưng nếu trời nắng, chúng ta có thể làm ướt cỏ bằng cách đổ nước từ vòi phun.

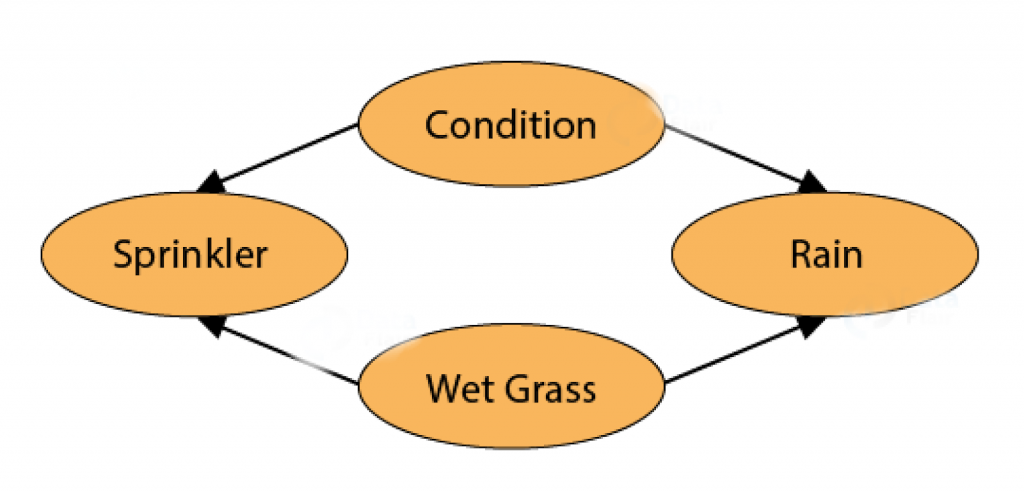
Khi xác suất của Mạng Bayes phản ánh thời tiết và bãi cỏ, thì BN có thể trả lời các câu hỏi như xác suất mưa hoặc vòi phun nước làm cho bãi cỏ ướt là bao nhiêu? Nếu xác suất mưa tăng lên, thì việc sử dụng vòi phun nước để tưới cỏ sẽ có tác động như thế nào?

Giả sử rằng cỏ ướt. Điều này có thể được góp phần bởi một trong hai lý do – Thứ nhất, trời mưa. Thứ hai, các vòi phun nước được bật. Sử dụng Quy tắc Baye, người ta có thể suy ra yếu tố góp phần nhiều nhất đối với cỏ ướt mà trong trường hợp này là do mưa.

Đặc điểm của Mạng Bayes trong R

Điều quan trọng là phải hiểu một số đặc điểm liên quan đến Bayesian Networks trong R . Chúng bao gồm những điều sau:

• Giải thích đi
• Lập luận từ trên xuống và từ dưới lên
• Thương vong
• Độc lập có điều kiện trong BN
• BN có nút rời rạc và liên tục
• Mô hình thời gian
• Mô hình Markov ẩn (HMM)
• Hệ thống động tuyến tính (LDS) và Bộ lọc Kalman

Giải thích Đi vắng

Trong ví dụ về hệ thống phun nước, hai nguyên nhân [Sprinkler (S) và Rain (R)] cạnh tranh để giải thích dữ liệu quan sát được. Con chung ‘W’ quan sát thấy rằng S và R trở nên phụ thuộc, mặc dù chúng độc lập. Hiện tượng này được gọi là giải thích đi vì một trong hai nguyên nhân là đủ để giải thích thực tế trên W. Trong ví dụ cỏ ướt, cỏ ướt cùng một lúc, đồng thời trời cũng đang mưa. Nó làm giảm xác suất hậu nghiệm.

Lập luận từ dưới lên và từ trên xuống

BN thường được gọi là mô hình phát triển vì chúng chỉ rõ cách các nguyên nhân tạo ra tác động. Trong ví dụ về vòi phun nước, bạn có bất kỳ bằng chứng nào về một hiệu ứng, đó là cỏ ướt, và bạn suy ra nguyên nhân có thể xảy ra nhất. Cách tiếp cận này được gọi là suy luận từ dưới lên hoặc suy luận chẩn đoán. Nó đi từ ảnh hưởng đến nguyên nhân và tạo ra một loại xác suất nghịch đảo. Trong biểu đồ BN, bạn có thể thực hiện suy luận từ dưới lên bằng cách đi qua các nút bằng chứng được kết nối thông qua các nút con của nó.

Từ trên xuống hoặc suy luận thông thường tính xác suất cỏ bị ướt khi trời có mây. Trong biểu đồ BN, đối với nút X, lý luận từ trên xuống có thể được thực hiện bằng cách đi qua các nút bằng chứng được kết nối thông qua các nút tổ tiên của nó.

Nguyên nhân

Các cuộc thảo luận về tai nạn giải thích nguyên nhân và kết quả của một hiện tượng. Ví dụ – Hiện tượng nào gây ra cái gì, các yếu tố chính đằng sau một hiệu ứng là gì? Trước đây, chúng tôi phải làm các thí nghiệm để suy ra thương vong trong một hiện tượng nhưng BNs đưa ra một nền tảng toán học vững chắc cho các cuộc thảo luận về thương vong mà không cần thử nghiệm.

Độc lập có điều kiện

Các Bayes ball thuật toán giải thích các mối quan hệ độc lập có điều kiện được mã hóa bởi một BN. Nó nói rằng hai tập hợp các nút A và B là độc lập cho một tập hợp C nếu không có cách nào để một quả bóng di chuyển từ A đến B trong đồ thị.

BN có nút rời rạc và liên tục

Ví dụ về vòi phun nước đã sử dụng các nút có giá trị phân loại và phân phối đa thức. Người dùng cũng có thể tạo BN với các nút có giá trị liên tục. Phân phối phổ biến nhất cho các biến này là Gaussian . Phân phối logistic hoặc softmax được sử dụng cho các nút rời rạc có cha mẹ liên tục. Bạn có thể tạo các mô hình phức tạp bằng cách sử dụng Gaussian đa thức, có điều kiện và phân phối logistic.

Mô hình thời gian

Bằng các mô hình đồ họa trực tiếp, các mô hình Thời gian thể hiện một quá trình dựa trên các đầu vào hoặc biến ngẫu nhiên. Các mô hình tạm thời là các mô hình đồ họa có hướng của các quá trình ngẫu nhiên. Chúng còn được gọi là BN động (DBN) . Các DBN đơn giản nhất là Mô hình Markov ẩn (HMM) và Hệ thống động tuyến tính (LDS) . Mô hình thời gian đơn giản hóa HMM và LDS bằng cách sử dụng trạng thái của các biến là ẩn hoặc quan sát.

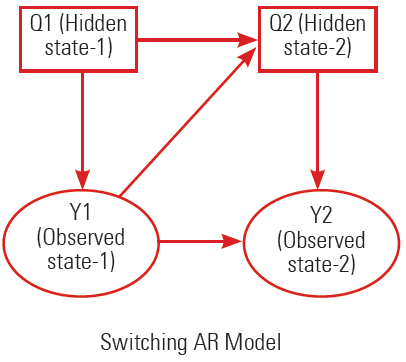
Mô hình Markov ẩn (HMM)

HMM có một nút ẩn rời rạc và một nút quan sát rời rạc hoặc liên tục trên mỗi lát. Hình dưới đây cho thấy một HMM:

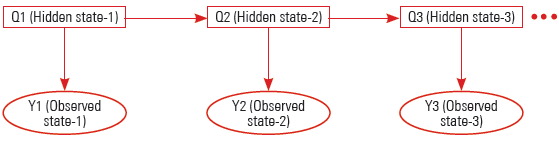
Biểu tượng vòng tròn đại diện cho các biến có giá trị liên tục. Biểu tượng hình vuông đại diện cho các biến có giá trị rời rạc. Tại đây, giải nén HMM cho các lát bốn lần. Việc sao chép phần thân của một vòng lặp nhiều lần được gọi là Unrolling. Các bản sao được sử dụng để thay thế nội dung gốc. Sự trùng lặp của các bản sao được gọi là hệ số hủy cuộn.

Để mô tả BDN, bạn phải thể hiện cấu trúc liên kết bên trong và giữa các lát cắt. Bạn cũng cần xác định các tham số cho 2 lát. Các mạng với hai lát cắt tạm thời như vậy còn được gọi là 2 TBN.

Hệ thống động tuyến tính (LDS) và Bộ lọc Kalman

Một LDS có cấu trúc liên kết giống như một HMM, nhưng nó giả định có tất cả các nút trong phân phối Gaussian tuyến tính. Phân phối tuyến tính-Gaussian như sau:

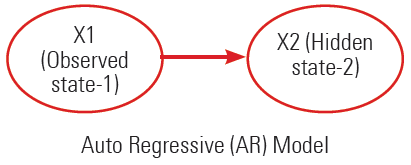
Mô hình hồi quy tự động

Các phương pháp Bayes là gì?

Có ba phương pháp khác nhau trong mạng Bayes:

• Loại bỏ biến
• Lập trình năng động
• Các thuật toán gần đúng

Hãy để chúng tôi thảo luận về các Phương pháp Bayesian này từng cái một:

Loại bỏ biến

Để thực hiện việc định biên hiệu quả, bạn có thể sử dụng Phân phối xác suất chung. Trong phương pháp này, bạn có thể tổng hợp các thuật ngữ không liên quan.

Ví dụ:

Chúng tôi sẽ xóa các biến từ trong ra ngoài. Bắt đầu với biến Xm và kết thúc với biến X1. Ở đây chúng tôi thực hiện các phép tính tổng từ phải sang trái, lưu trữ các kết quả trung gian (hệ số) để tránh tính toán lại. Để loại bỏ biến Xi, chúng tôi bắt đầu bằng cách thu thập tất cả các yếu tố đề cập đến Xi và loại bỏ chúng khỏi tập hợp các yếu tố của chúng tôi. Trong quá trình tính toán, độ phức tạp của việc loại bỏ biến phụ thuộc vào kích thước của yếu tố lớn nhất. Điều này, đến lượt nó, phụ thuộc vào thứ tự loại bỏ các biến. Trong mạng cây đa, độ phức tạp không gian và thời gian là tuyến tính trong kích thước của mạng.

Lập trình động

Giả sử bạn muốn tính toán một số lợi nhuận. Nếu bạn sử dụng thuật toán loại bỏ biến, thì sẽ có một số phép tính dư thừa. Để tránh chúng, bạn có thể sử dụng phương pháp Lập trình động (DP) . Nó hoạt động theo kiểu mô hình đồ họa.

Khi đồ thị Mạng Bayes có dạng xoay vòng (nghĩa là dạng cây), thì bạn có thể sử dụng thuật toán truyền thông điệp cục bộ. Đây là một thuật toán chuyển tiếp-lùi đơn giản cho chuỗi HMM . Khi Mạng Bayes có các chu kỳ vô hướng, sẽ có nguy cơ tính hai lần bởi các thuật toán truyền thông điệp cục bộ. Để tránh điều này, bạn có thể chuyển đổi Mạng Bayes không định hướng thành một cây bằng cách nhóm các nút lại với nhau. Do đó, cây kết quả được gọi là cây nối.

Nhược điểm lớn của thuật toán Lập trình động là mất nhiều thời gian hơn để chạy ở kích thước cụm lớn. Cảm ứng cho độ rộng của kích thước đồ thị đề cập đến sự gia tăng thời gian xử lý. Giảm thiểu chiều rộng của đồ thị là một bài toán khó NP . NP là một loại các bài toán tính toán. Bạn có thể giải quyết vấn đề này với sự trợ giúp của máy Turing không xác định.

Tìm hiểu về các ứng dụng mạng Bayes trong thế giới thực hàng đầu

Các thuật toán xấp xỉ

Các mô hình có cấu trúc lặp lại như mô hình chuỗi thời gian đa biến được sử dụng để phân tích hình ảnh và có độ rộng cảm ứng cao. Vì vậy, chúng sẽ mất rất nhiều thời gian nếu bạn cố gắng suy luận chúng bằng thuật toán loại bỏ biến hoặc lập trình động.

Đối với những mô hình này, bạn cũng có thể sử dụng kỹ thuật xấp xỉ. Hãy để chúng tôi xem một số kỹ thuật xấp xỉ chính

Phương pháp biến đổi

Đây là một trong những kỹ thuật trường trung bình đơn giản nhất được sử dụng để tính gần đúng của các thuật toán. Nó sử dụng quy tắc xấp xỉ tổng của các biến ngẫu nhiên có giá trị lớn bằng cách sử dụng phương tiện của chúng.

Phương pháp lấy mẫu (Monte Carlo)

Đây là kiểu lấy mẫu quan trọng đơn giản nhất. Phương pháp chung là:

• Xác định các mẫu x từ P (x).
• Kiểm tra các mẫu bằng cách sử dụng khả năng P (x hoặc y) của chúng

Truyền bá niềm tin vòng lặp

Trong phương pháp này, đồ thị thực tế áp dụng thuật toán ngọc trai. Điều này dẫn đến việc đếm gấp đôi. Nó đã được quan sát thấy rằng các sự cố được tính hai lần được hủy bỏ và đưa ra kết quả chính xác.

Điều hòa đường cắt có giới hạn

Bạn có thể phá vỡ các vòng lặp trong biểu đồ bằng cách khởi tạo các tập hợp con của các biến. Quá trình này diễn ra rất chậm trong trường hợp bộ cắt lớn. Để tính toán điều này, giới hạn thấp hơn khởi tạo một tập hợp con của các giá trị tập hợp cắt.

Phương pháp xấp xỉ tham số

Triệu hồi trung gian ở dạng đơn giản và dễ hiểu. Ví dụ, Nhóm nhỏ và thuật toán Boyen-Koller.

Nghiên cứu điển hình về Đường sắt Queensland

Mạng Bayes được sử dụng rộng rãi để lập luận với sự không chắc chắn. Trong đó, các nguồn thông tin khác nhau được kết hợp để củng cố các hệ thống hỗ trợ thông minh. Bayesian Networks làm việc chặt chẽ với miền và do đó yêu cầu chuyên môn của những người có kiến ​​thức cần thiết. Trong nghiên cứu điển hình này, chúng ta sẽ thảo luận về cách Bayesian Networks đang được sử dụng để xây dựng sự hài lòng của khách hàng nhằm hỗ trợ các quyết định quản lý trong hệ thống vận tải.

Tại Queensland Rails, Australia, sự hài lòng của khách hàng là một Chỉ số Hiệu suất Chính (KPI) chính thúc đẩy hoạt động kinh doanh của họ. Theo truyền thống, Đường sắt Queensland sử dụng trả lời bảng câu hỏi để khảo sát ý kiến ​​của hành khách. Tuy nhiên, điều này tỏ ra không hiệu quả trong việc đánh giá ý kiến ​​chung hoặc thu thập thông tin chi tiết về dịch vụ của họ để cải thiện hơn nữa. Với sự trợ giúp của Bayesian Networks, họ có thể đáp ứng những yêu cầu này.

Dữ liệu được sử dụng để phát triển Mô hình Bayes bao gồm các bảng câu hỏi. Các câu hỏi được giải quyết là về các thuộc tính và yếu tố của dịch vụ khách hàng. Các yếu tố này được chia thành hai mức thời gian cao điểm và thấp điểm. Hơn nữa, đối với mỗi yếu tố, phản hồi của khách hàng được quy cho loại Trải nghiệm tích cực, tiêu cực hoặc trung lập. Các yếu tố ảnh hưởng đến trải nghiệm của khách hàng như Thành phần hành trình và Thành phần toàn diện.

Các Thành phần Hành trình chịu ảnh hưởng nhiều hơn bởi các yếu tố như Vận chuyển, Cơ sở Nhà ga, Thông tin Vận hành, v.v. Các Thành phần Toàn diện bị ảnh hưởng bởi Yếu tố Dịch vụ và Yếu tố Hành khách. Ba trạng thái xác suất được sử dụng để thiết kế mỗi nút – Tích cực, Tiêu cực và Trung tính. Cuối cùng, mối quan hệ giữa các mô hình này đã được thiết lập. Hình ảnh trực quan sau đây cung cấp một ví dụ về một trong các thành phần của mô hình được sử dụng để đưa ra các suy luận về sự hài lòng của khách hàng:

Sau khi tiến hành phân tích mức độ ảnh hưởng trên mô hình, chúng tôi kết luận rằng nút Thành phần hành trình có ảnh hưởng mạnh hơn đến nút Sự hài lòng của khách hàng so với nút Thành phần toàn diện. Hơn nữa, các thành phần trạm có ảnh hưởng tối đa đến nút Thành phần Hành trình. Cuối cùng, các kịch bản được xác định bởi Đường sắt Queensland và những thay đổi do đó trong xác suất của mô hình đã được quan sát. Một số kịch bản là – cải thiện cơ sở hạ tầng, tăng giá vé, giảm độ an toàn, v.v.

Bản tóm tắt

Trong hướng dẫn về Mạng Bayes này, chúng tôi đã thảo luận về Thống kê Bayes và Mạng Bayes. Hơn nữa, chúng tôi đã xem các ví dụ và đặc điểm của Mạng Bayesian của Mạng Bayes.