Lý thuyết Đồ thị hàm số y = ax (mới 2022 + Bài Tập) – Toán 9

Lý thuyết Đồ thị hàm số y = ax lớp 9 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 9 Bài 3: Đồ thị hàm số y = ax.

Lý thuyết Toán 9 Bài 3: Đồ thị hàm số y = ax

A. Lý thuyết

1. Đồ thị hàm số y = ax + b (a ≠ 0)

Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:

– Cắt trục tung tại điểm có tung độ bằng b.

– Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0

Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.

Ví dụ 1. Gọi A là giao điểm của hai đường thẳng y = x − 1 và y = 3x + 1, tìm tọa độ của điểm A?

Lời giải:

Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:

x − 1 = 3x + 1

⇔ 3x − x = − 1 − 1

⇔ 2x = − 2

⇔ x = − 1.

Với x = − 1 thì y = − 1 − 1 = − 2. Khi đó, A(− 1; − 2).

Vậy tọa độ giao điểm A(− 1; − 2).

2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)

• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).

• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.

Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.

Cho y = 0 thì x=− ba, ta được điểm Q−ba;  0 thuộc trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).

 Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.

Ví dụ 2. Vẽ đồ thị hàm số y = 2x – 1.

Bước 1: Cho x = 0 thì y = −1, ta được điểm A(0; −1) ∈ Oy.

Cho y = 1 thì 2x – 1 = 1 ⇔ x = 1, ta được điểm B(1; 1)

Bước 2: Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = 2x – 1.

Ta có đồ thị hàm số:

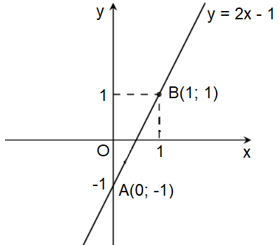
B. Bài tập tự luyện

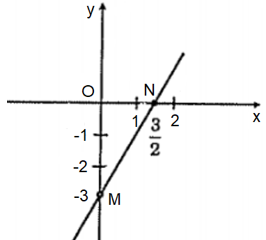
Bài 1. Vẽ đồ thị hàm số y = 2x – 3.

Lời giải:

Vẽ đồ thị hàm số y = 2x – 3.

Bước 1: Cho x = 0 thì y = −3, ta được điểm M(0; −3) ∈ Oy.

Cho y = 0 thì x = 2x – 3 = 0 ⇔x=32, ta được điểm N32;  0.

Bước 2: Vẽ đường thẳng đi qua hai điểm M và N, ta được đồ thị hàm số y = 2x – 3.

Ta có đồ thị hàm số:

Bài 2. Cho tọa độ hai điểm A−13;  5;   B52;  2.

Hỏi điểm nào thuộc đồ thị hàm số y = − 3x + 4?

Lời giải:

* Với A−13;  5: Thay xA=−13 vào hàm số y = − 3x + 4.

Ta được: y=(− 3)  .  −13+4=1+4=5.

Do đó, điểm A−13;  5 thuộc đồ thị hàm số y = − 3x + 4.

* Với B52;  2: Thay xA=52 vào hàm số y = − 3x + 4.

Ta được: y=(− 3)  .  52+4=− 152+4=− 72 ≠ 2.

Do đó, điểm B52;  2 không thuộc đồ thị hàm số y = − 3x + 4.

Vậy điểm A−13;  5 thuộc đồ thị hàm số y = − 3x + 4.

Trắc nghiệm Toán 9 Bài 3: Đồ thị của hàm số y = ax + b

Câu 1: Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a≠0)

A. Là đường thẳng đi qua gốc tọa độ

B. Là đường thẳng song song với trục hoành

C. Là đường thẳng đi qua hai điểm A (0; b), B−ba;0 với b≠0 

D. Là đường cong đi qua gốc tọa độ

Hiển thị đáp án  

Đáp án: C

Giải thích:

Đồ thị hàm số y = ax + b (a ≠0) là một đường thẳng

Trường hợp 1:

Nếu b = 0, ta có hàm số y = ax.

Đồ thị của y = ax là một đường thẳng đi qua gốc tọa độ O (0; 0) và điểm A (1; a)

Trường hợp 2:

Nếu b ≠0 thì đồ thị của y = ax là một đường thẳng đi qua các điểm A (0; b), B−ba;0

Câu 2: Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a ≠0) với b = 0

A. Là đường thẳng đi qua gốc tọa độ

B. Là đường thẳng song song với trục hoành

C. Là đường thẳng đi qua hai điểm A (1; b), B−ba;0 

D. Là đường cong đi qua gốc tọa độ

Hiển thị đáp án  

Đáp án: A

Giải thích:

Đồ thị hàm số y = ax + b (a≠0) là một đường thẳng

Trường hợp 1:

Nếu b = 0, ta có hàm số y = ax.

Đồ thị của y = ax là một đường thẳng đi qua gốc tọa độ O (0; 0) và điểm A (1; a)

Trường hợp 2: Nếu b ≠0 thì đồ thị của y = ax là một đường thẳng đi qua các điểm A (0; b), B−ba;0

Câu 3: Cho ba đường thẳng d1: y = −2x; d2: y = −3x – 1; d3: y = x + 3

Khẳng định nào dưới đây là đúng?

A. Giao điểm của d1 và d3 là A (2; 1)

B. Ba đường thẳng trên không đồng quy

C. Đường thẳng d2 đi qua điểm B (1; 4)

D. Ba đường thẳng trên đồng quy tại điểm M (−1; 2)

Hiển thị đáp án  

Đáp án: D

Giải thích:

+) Thay tọa độ điểm A (2; 1) vào phương trình đường thẳng d1 ta được:

1 = −2.2⇔1 = −4 (vô lý) nên A ∉d1

hay A (2; 1) không là giao điểm của d1 và d3.

Suy ra A sai.

+) Thay tọa độ điểm B (1; 4) vào phương trình đường thẳng d2 ta được:

4 = −3.1− 4 ⇔4 = −4 (vô lý) nên B ∉d2.

Suy ra C sai

+) Xét tính đồng quy của ba đường thẳng:

* Phương trình hoành độ giao điểm của d1 và d2:

−2x = −3x −1⇔ x = −1

⇒y = −2. (−1)⇔ y = 2

Suy ra tọa độ giao điểm của d1 và d­2 là: (−1; 2)   

* Thay x = −1; y = 2 vào phương trình đường thẳng d3 ta được 2 = −1 + 3

⇔2 = 2 (luôn đúng)

Vậy ba đường thẳng trên đồng quy tại điểm M (−1; 2)

Câu 4: Cho đường thẳng d: y = −3x + 2. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Tính diện tích tam giác OAB.

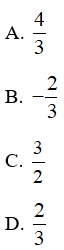
Hiển thị đáp án  

Đáp án: D

Giải thích:

Câu 5: Đồ thị hàm số y = 3 (x – 1) +43 đi qua điểm nào dưới đây?

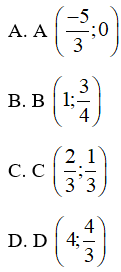
Hiển thị đáp án  

Đáp án: C

Giải thích:

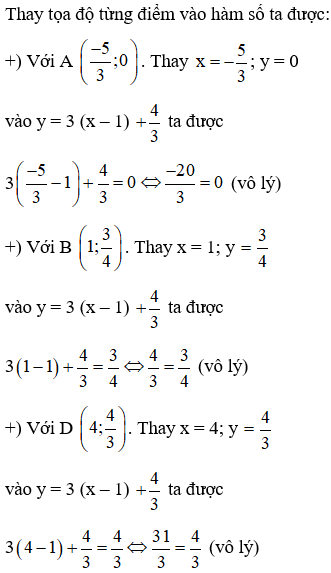
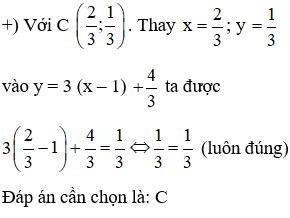
Câu 6: Cho hai đường thẳng d1: y = 2x – 2 và d2: y = 3 – 4x. Tung độ giao điểm của d1; d2 có tọa độ là:

A. y=−13

B. y=23

C. y = 1

D. y = −1

Hiển thị đáp án  

Đáp án: A

Giải thích:

Câu 7: Cho đường thẳng d: y = 2x + 6. Giao điểm của d với trục tung là:

A. P 0;16 

B. N (6; 0)

C. M (0; 6)

D. D (0; −6)

Hiển thị đáp án  

Đáp án: C

Giải thích:

Câu 8: Cho hàm số y = (1 – m) x + m. Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = −3

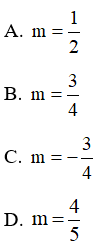
Hiển thị đáp án  

Đáp án: B

Giải thích:

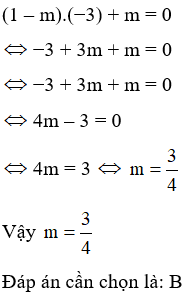
Câu 9: Với giá trị nào của m thì ba đường thẳng d1: y = 6 − 5x; d2: y = (m + 2)x + m và d3: y = 3x + 2 đồng quy?

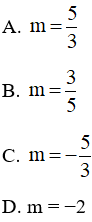
Hiển thị đáp án  

Đáp án: A

Giải thích:

Câu 10: Trong các hình vẽ sau, hình vẽ nào là đồ thị của hàm số y = 3x – 2

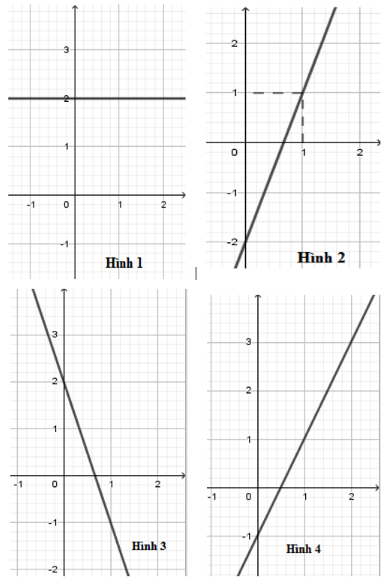
A. Hình 4

B. Hình 2

C. Hình 3

D. Hình 1

Hiển thị đáp án  

Đáp án: B

Giải thích:

Đồ thị hàm số y = 3x − 2 là đường thẳng đi qua hai điểm có tọa độ (0; −2) và (1; 1) nên hình 2 là đồ thị hàm số y = 3x − 2.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

Lý thuyết Đường thẳng song song và đường thẳng cắt nhau

Lý thuyết Hệ số góc của đường thẳng y = ax

Lý thuyết Ôn tập chương II

Lý thuyết Các khái niệm về hàm số

Lý thuyết Hàm số bậc nhất