Khảo sát sự biến thiên và vẽ đồ thị hàm số – Giải Toán 12

Nội dung hướng dẫn giải bài tập SGK Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số lớp 12 sẽ hỗ trợ các em phương pháp khảo sát các đồ thi hàm số bậc 2, hàm số bậc 3, hàm số bậc 4 hay và hiệu quả nhất.

Tham khảo thêm một số tài liệu học tập lớp 12 (được xem nhiều):

Giải Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số

Trả lời câu hỏi SGK Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 32: 

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số đã học theo sơ đồ trên.

y = ax + b

y = ax2 + bx + c

Lời giải:

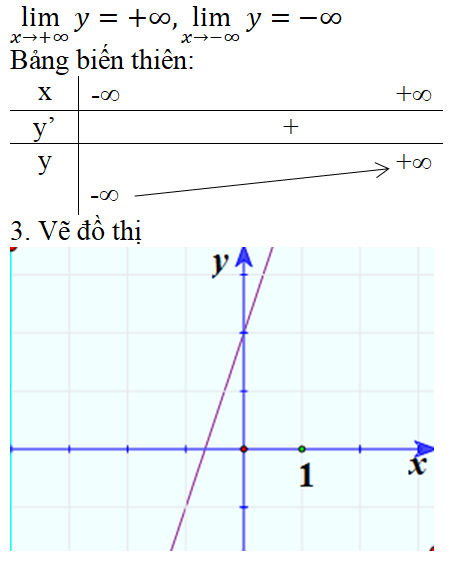
* Hàm số y = ax + b

Trường hợp a > 0

1. TXĐ: D = R.

2. Sự biến thiên.

y’ = a > 0. Vậy hàm số đồng biến trên toàn bộ R.

Trường hợp a < 0

1. TXĐ: D = R.

2. Sự biến thiên.

y’ = a < 0. Vậy hàm số đồng biến trên toàn bộ R.

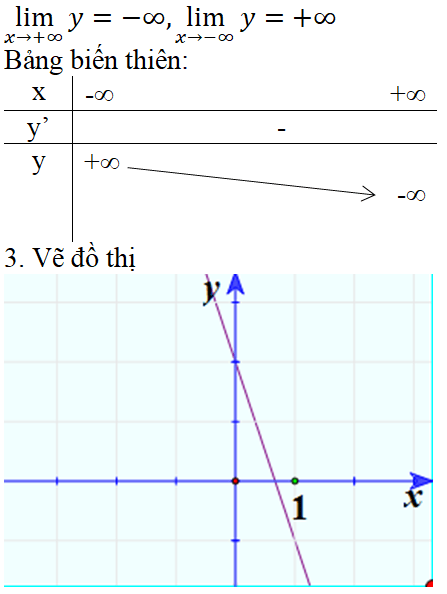
* Hàm số y = ax2 + bx + c

Trường hợp a > 0

1. TXĐ: D = R.

2. Sự biến thiên.

y’ = 2ax + b. Cho y’ = 0 thì x = – b/2a.

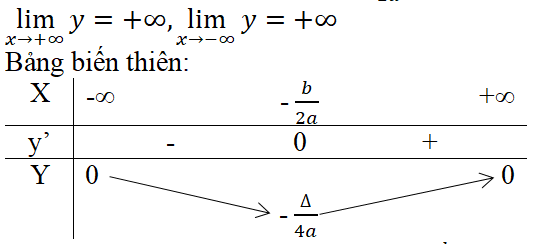
Hàm số nghịch biến trên khoảng (-∞,- b/2a).

Hàm số đồng biến trên khoảng [- b/2a, +∞].

Hàm số đạt cực tiểu bằng – Δ/4a tại x = – b/2a .

3. Vẽ đồ thị:

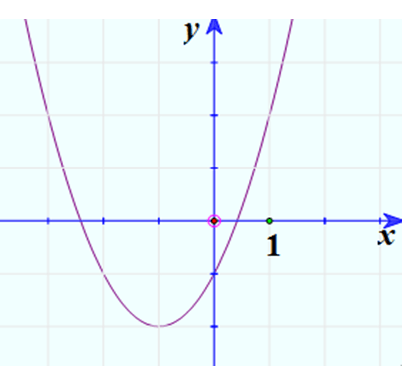
Trường hợp a < 0

1. TXĐ: D = R.

2. Sự biến thiên.

y’ = 2ax + b. Cho y’ = 0 thì x = – b/2a.

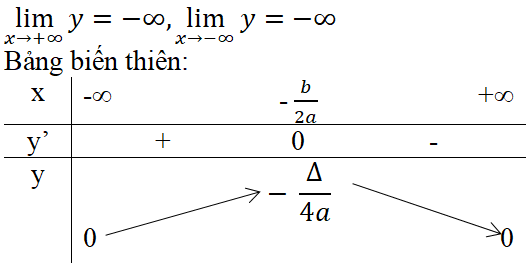
Hàm số đồng biến trên khoảng (-∞,- b/2a).

Hàm số nghịch biến trên khoảng [- b/2a, +∞].

Hàm số đạt cực đại bằng – Δ/4a tại x = – b/2a .

3. Vẽ đồ thị:

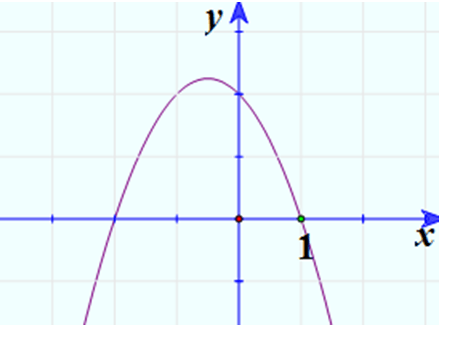
Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 33:

Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x3 + 3×2 – 4. Nêu nhận xét về đồ thị của hàm số này với đồ thị của hàm số khảo sát trong Ví dụ 1.

Lời giải:

1.TXĐ: D = R.

2. Sự biến thiên:

y’ = -3×2 + 6x. Cho y’ = 0 ⇒ x = 0 hoặc x = 2.

Bảng biến thiên:

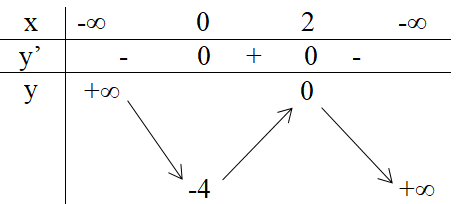
Hàm số đồng biến trên khoảng (0,2)

Hàm số nghịch biến trên các khoảng (-∞,0), (2,+ ∞).

Hàm số đạt cực đại bằng 0 tại x = 2.

Hàm số đạt cực tiểu bằng -4 tại x = 0.

3. Đồ thị

Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 35: 

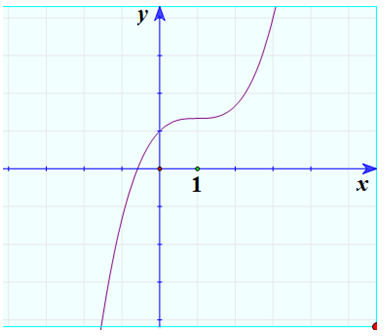
Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x3/3 – x2 + x + 1.

Lời giải:

1.TXĐ: D = R.

2. Sự biến thiên:

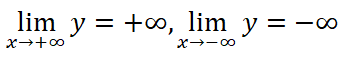
y’ = x2 – 2x + 1 = (x – 1)2 ≥ 0 với mọi x. Vậy hàm số đồng biến trên toàn bộ R.

Cho y’ = 0 ⇒ x = 1.

Bảng biến thiên

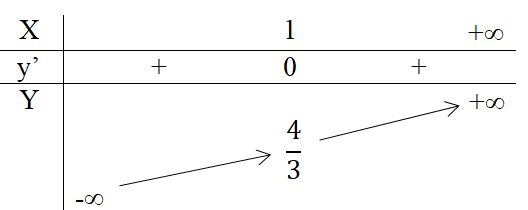
3. Đồ thị

Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 36: 

Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x4 + 2×2 + 3.

Bằng đồ thị, biện luận theo m số nghiệm của phương trình -x4 + 2×2 + 3 = m.

Lời giải:

1.TXĐ: D = R.

2. Sự biến thiên:

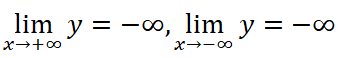
y’ = -4×3 + 4x. Cho y’ = 0 ⇒ x = 0 hoặc x = ±1.

Bảng biến thiên:

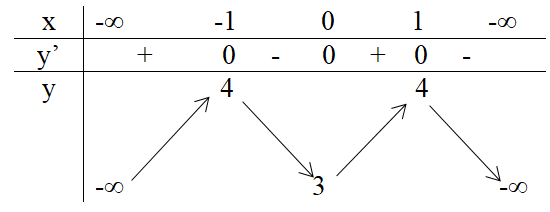
Hàm số đồng biến trên: (-∞,-1), (0,1).

Hàm số nghịch biến trên: (-1,0), (1, +∞).

Hàm số đạt cực đại bằng 4 tại x = -1 và x = 1.

Hàm số đạt cực tiểu bằng 3 tại x = 0.

3. Đồ thị

Giải biện luận phương trình -x4 + 2×2 + 3 = m.

Số giao điểm của hai đồ thị y = -x4 + 2×2 + 3 và y = m là số nghiệm của phương trình trên.

Với m > 4. Hai đồ thị không giao nhau nên phương trình vô nghiệm.

Với m = 4 và m < 3. Hai đồ thị giao nhau tại 2 điểm phân biệt nên phương trình có hai nghiệm phân biệt.

Với m = 3. Hai đồ thị giao nhau tại 3 điểm phân biệt nên phương trình có ba nghiệm phân biệt.

Với 3 < m < 4. Hai đồ thị giao nhau tại 4 điểm phân biệt nên phương trình có bốn nghiệm phân biệt.

Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 38: 

Lấy một ví dụ về hàm số dạng y = ax4 + bx2 + c sao cho phương trình y’ = 0 chỉ có một nghiệm.

Lời giải:

Ví dụ hàm số y = x4. Có đạo hàm y’ = 4×3. Cho y’ = 0 thì x = 0.

Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 42: 

Tìm tọa độ giao điểm của đồ thị hai hàm số

y = x2 + 2x – 3

y = -x2 – x + 2.

Lời giải:

Xét phương trình tương giao:

-x2 – x + 2 = x2 + 2x – 3 ⇔ 2×2 + 3x – 5 = 0

⇔ x = 1 hoặc x = -5/2.

Vậy tọa độ giao điểm là (1, 0) và (-5/2, 8.25).

Giải bài tập SGK Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 1 (trang 43 SGK Giải tích 12): 

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:

a) y = 2 + 3x – x3 ;

b) y = -x3 + 4×2 – 4x

c) y = x3 + x2 + 9x ;

d) y = -2×3 + 5

Lời giải:

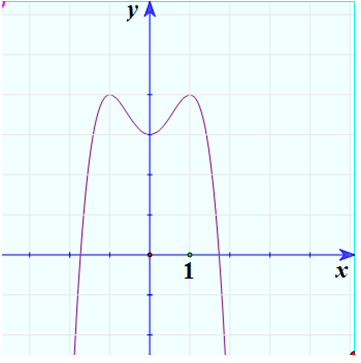
a) Hàm số y = -x3 + 3x + 2.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y’ = -3×2 + 3.

y’ = 0 ⇔ x = ±1.

Trên các khoảng (-∞; -1) và (1; +∞), y’ < 0 nên hàm số nghịch biến.

Trên (-1 ; 1), y’ > 0 nên hàm số đồng biến.

+ Cực trị :

Hàm số đạt cực đại tại x = 1, yCĐ = 4 ;

Hàm số đạt cực tiểu tại x = -1 ; yCT = 0.

+ Giới hạn:

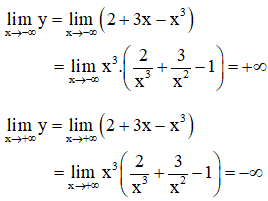
+ Bảng biến thiên:

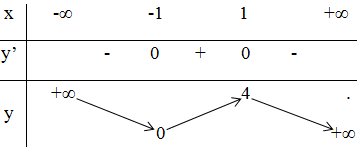
3) Đồ thị:

Ta có : 2 + 3x – x3 = 0 ⇔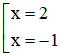 

Vậy giao điểm của đồ thị với trục Ox là (2; 0) và (-1; 0).

y(0) = 2 ⇒ giao điểm của đồ thị với trục Oy là (0; 2).

Đồ thị hàm số :

b) Hàm số y = -x3 + 4×2 – 4x.

1) Tập xác định: D = R

2) Sự biến thiên:

y’ = -3×2 + 8x – 4;

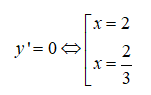
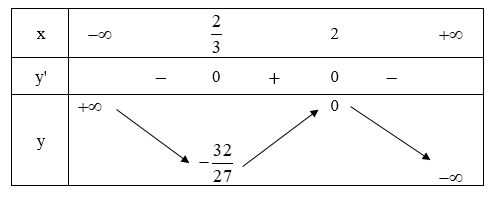
Trên các khoảng (-∞; 2/3) và (2; +∞) thì y’ < 0 nên hàm số nghịch biến.

Trên (2/3; 2) thì y’ > 0 nên hàm số đồng biến.

+ Cực trị:

Hàm số đạt cực đại tại x = 2, fCD = 0;

Hàm số đạt cực tiểu tại x = 2/3; fCT = -32/27

+ Giới hạn:

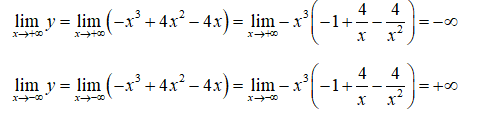
+ Bảng biến thiên:

3) Đồ thị:

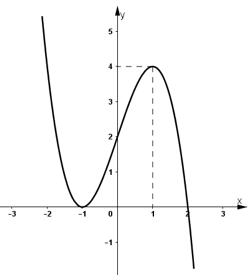
Ta có : -x3 + 4×2 – 4x = 0 ⇔ -x(x – 2)2 = 0 ⇔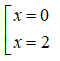 

Vậy giao điểm của đồ thị với Ox là (0;0) và (2;0).

+ y(1) = -1. Vậy (1; -1) thuộc đồ thị hàm số.

+ y(3) = -3. Vậy (3;-3) thuộc đồ thị hàm số

y(-1) = -1 ⇒ (-1; -1) thuộc đồ thị hàm số

Đồ thị hàm số :

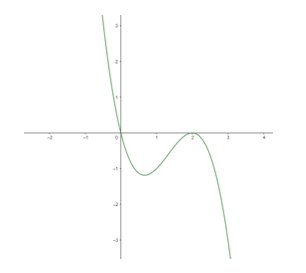
c) Hàm số y = x3 + x2 + 9x.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y’ = 3×2 + 2x + 9 > 0

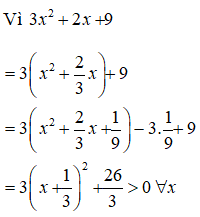
⇒ Hàm số luôn đồng biến trên R.

+ Hàm số không có cực trị.

+ Giới hạn:

+ Bảng biến thiên:

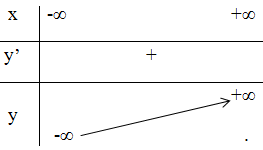
3) Đồ thị hàm số.

+ Đồ thị hàm số cắt trục Ox tại (0 ; 0).

+ Đồ thị hàm số đi qua (1; 11) ; (-1; -9)

d) Hàm số y = 2×3 + 5.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y’ = 6×2 ≥ 0 ∀ x ∈ R

Hàm số đồng biến trên R

Hàm số không có cực trị.

+ Giới hạn:

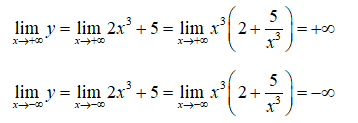
+ Bảng biến thiên:

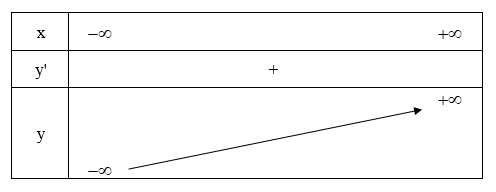
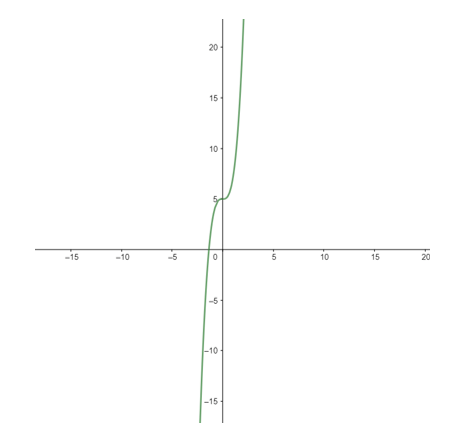
3) Đồ thị:

Đồ thị hàm số cắt trục tung tại (0;5)

Đồ thị hàm số đi qua điểm (1;7) và (-1;3)

Bài 2 (trang 43 SGK Giải tích 12): 

Khảo sát tự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:

Lời giải:

a) Hàm số y = -x4 + 8×2 – 1.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y’ = -4×3 + 16x = -4x(x2 – 4)

y’ = 0 ⇔ -4x(x2 – 4) = 0 ⇔ x = 0 ; x = ±2

Trên khoảng (-∞; -2) và (0; 2), y’ > 0 nên hàm số đồng biến.

Trên các khoảng (-2; 0) và (2; +∞), y’ < 0 nên hàm số nghịch biến.

+ Cực trị :

Hàm số đạt cực đại tại x = 2 và x = -2 ; yCĐ = 15

Hàm số đạt cực tiểu tại x = 0 ; yCT = -1.

+ Giới hạn:

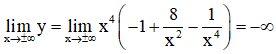
+ Bảng biến thiên:

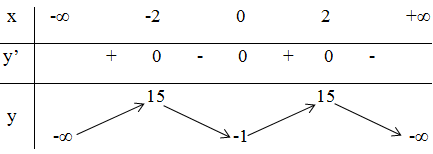
3) Đồ thị:

+ Hàm số đã cho là hàm số chẵn, vì:

y(-x) = -(-x)4 + 8(-x)2 – 1 = -x4 + 8×2 – 1 = y(x)

⇒ Đồ thị nhận Oy làm trục đối xứng.

+ Giao với Oy tại điểm (0; -1) (vì y(0) = -1).

+ Đồ thị hàm số đi qua (-3; -10) và (3; 10).

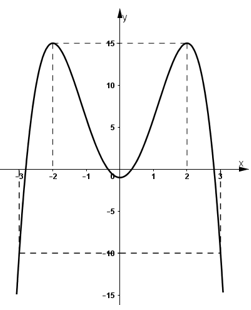
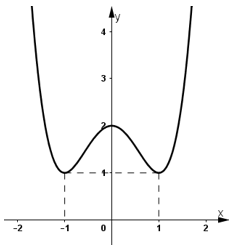
b) Hàm số y = x4 – 2×2 + 2.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y’ = 4×3 – 4x = 4x(x2 – 1)

y’ = 0 ⇔ 4x(x2 – 1) = 0 ⇔ x = 0 ; x = ±1.

+ Giới hạn:

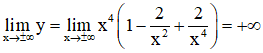
+ Bảng biến thiên:

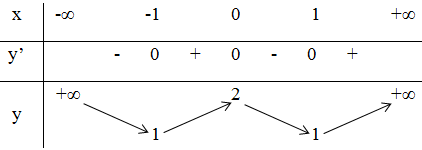
Kết luận :

Hàm số đồng biến trên khoảng (-1; 0) và (1; +∞).

Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1).

Đồ thị hàm số có hai điểm cực tiểu là: (-1; 1) và (1; 1).

Đồ thị hàm số có điểm cực đại là: (0; 2)

3) Đồ thị:

+ Hàm số chẵn nên đồ thị hàm số nhận trục Oy là trục đối xứng.

+ Đồ thị hàm số cắt trục tung tại (0; 2).

+ Đồ thị hàm số đi qua (-1; 1) và (1; 1).

+ Đồ thị hàm số:

c) Hàm số 

1) Tập xác định: D = R

2) Sự biến thiên:

+ y’ = 2×3 + 2x = 2x(x2 + 1)

   y’ = 0 ⇔ 2x(x2 + 1) = 0 ⇔ x = 0

+ Giới hạn:

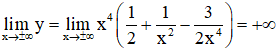
+ Bảng biến thiên:

Kết luận: Hàm số đồng biến trên khoảng (0; +∞).

Hàm số nghịch biến trên các khoảng (-∞; 0).

Đồ thị hàm số có điểm cực đại là: (0; -3/2).

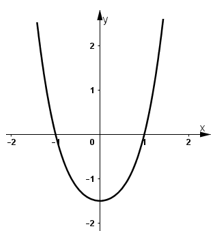
3) Đồ thị:

+ Hàm số chẵn nên nhận trục Oy là trục đối xứng.

+ Hàm số cắt trục hoành tại điểm (-1; 0) và (1; 0).

+ Hàm số cắt trục tung tại điểm  (0;-3/2)

d) Hàm số y = -2×2 – x4 + 3.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y’ = -4x – 4×3 = -4x(1 + x2)

y’ = 0 ⇔ -4x(1 + x2) = 0 ⇔ x = 0

+ Giới hạn:

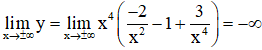
+ Bảng biến thiên:

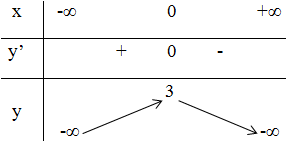
Kết luận: Hàm số đồng biến trên khoảng (-∞; 0).

Hàm số nghịch biến trên các khoảng (0; +∞).

Đồ thị hàm số có điểm cực đại là: (0; 3).

3) Đồ thị:

+ Hàm số là hàm số chẵn nên nhận trục Oy là trục đối xứng.

+ Hàm số cắt trục Ox tại (-1; 0) và (1; 0).

+ Hàm số cắt trục Oy tại (0; 3).

Nội dung giải bài tập SGK Bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số còn tiếp, mời các em xem full tại file tải về miễn phí…

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập SGK Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số file Word, pdf hoàn toàn miễn phí!