Khái niệm 2 tam giác đồng dạng là gì? Bài tập, cách chứng minh

Hai tam giác đồng dạng là kiến thức quan trọng có trong chương trình Toán học THCS. Nếu như bạn chưa hiểu rõ khái niệm 2 tam giác đồng dạng là gì, bài tập, cách chứng minh… thì đừng bỏ qua các thông tin trong bài viết này của caunang.com.vn.

Khái niệm 2 tam giác đồng dạng là gì?

Hai tam giác đồng dạng khi các góc của hai tam giác tương ứng với nhau và có các cạnh tương ứng tỉ lệ với nhau.

Tam giác A’B’C là tam giác đồng dạng với tam giác ABC khi:

Về góc: A = A’; B = B’; C = C’

Về cạnh: ABA’B’ = BCB’C’ = CAC’A’

=> Khi đó hai tam giác sẽ được kí hiệu đồng dạng với nhau: ABC ~ A’B’C’

Tính chất tam giác đồng dạng

2 tam giác đồng dạng suy ra được gì? Từ hai tam giác đồng dạng chúng ta suy ra được:

Mỗi tam giác sẽ đồng dạng với chính nó ABC ~ ABC.

Tính chất giao hoán: Nếu như tam giác A’B’C’ đồng dạng với tam giác ABC thì tam giác ABC cũng sẽ đồng dạng với tam giác A’B’C’.

Tính chất bắc cầu: Nếu như tam giác A’B’C’ đồng dạng với tam giác A’’B’’C’’, còn tam giác A’’B’’C’’ đồng dạng với tam giác ABC thì ta sẽ có cặp tam giác đồng dạng A’B’C’ và ABC.

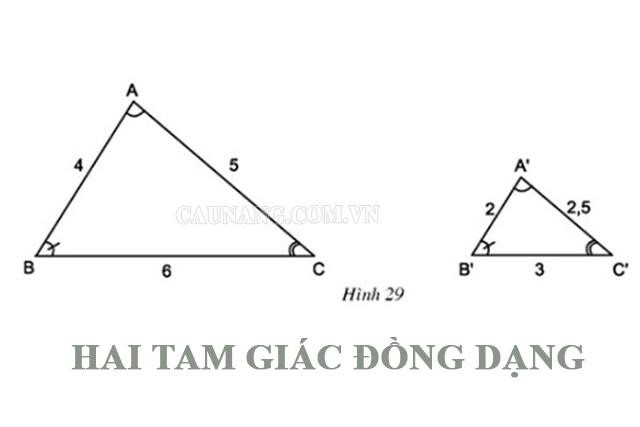
Định lý về 2 tam giác đồng dạng

Nếu một đường thẳng cắt hai cạnh của tam giác và nó song song với cạnh còn lại thì nó sẽ tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Định lý này cũng đúng trong trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác và nó song song với cạnh còn lại.

Các trường hợp tam giác đồng dạng

Dưới đây là 3 trường hợp hai tam giác đồng dạng mà bất kỳ ai cũng đã được học, như sau:

Trường hợp 1: Cạnh – cạnh – cạnh

Hai tam giác đồng dạng với nhau với nhau nếu ba cạnh của tam giác này bằng với ba cạnh của tam giác kia. Trong trường hợp này, chúng ta không cần so sánh giá trị góc của hai tam giác với nhau.

Ví dụ: Cho 2 tam giác ABC và A’B’C’ đồng dạng với nhau thì suy ra AB =A’B’; BC =B’C’; AC = A’C’.

Trường hợp 2: Góc – góc

Hai tam giác đồng dạng vuông góc với nhau nếu như một trong hai cặp góc hoặc cặp cạnh của chúng tương ứng với nhau.

Trường hợp 3: Góc – cạnh – góc

Trong trường hợp góc – cạnh – góc, 2 tam giác đồng dạng với nhau khi hai góc và cạnh bên của chúng bằng nhau. Hoặc hiểu theo cách khác thì hai tam giác đồng dạng khi hai cạnh của nó có tỉ lệ bằng nhau, góc xen giữa hai cạnh của hai cạnh cũng bằng nhau.

Ví dụ: 2 tam giác ABC và A’B’C’ đồng dạng với nhau khí:

ABA’B’ = ACA’C’ và A = A’ => Tam giác A’B’C’ đồng dạng với tam giác ABC.

Các định lí 2 tam giác vuông đồng dạng

Định lí 1: Nếu canh góc vuông và cạnh huyền của tam giác này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác kia thì hai tam giác vuông đó sẽ đồng dạng với nhau.

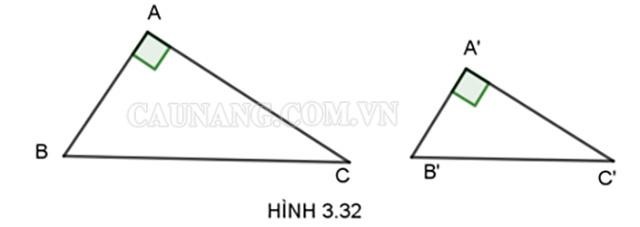
Định lí 2: Nếu như hai cạnh góc vuông của tam giác này tỉ lệ lại với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông này đồng dạng với nhau.

Định lí 3: Nếu như góc nhọn của hai tam giác bằng nhau thì hai tam giác vuông đó sẽ là hai tam giác đồng dạng.

Cách chứng minh tam giác đồng dạng lớp 9

Cách 1: Hai tam giác được coi là đồng dạng nếu như chúng có các cặp cạnh tương ứng tỉ lệ và có các góc tương ứng tỉ lệ.

Cách 2: Định lý Talet: Nếu như một đường thẳng song song với một cạnh của tam giác và nó cắt hai cạnh còn lại thì sẽ vạch ra trên cạnh đó các đoạn thẳng tương ứng tỷ lệ.

Cách 3: Chứng minh điều kiện cần và đủ để hai tam giác đồng dạng: Hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng. Hai tam giác có hai cặp góc tương ứng bằng nhau thì nó cũng đồng dạng. Hai tam giác có hai cặp cạnh cạnh tương ứng tỉ lệ, hai góc xen giữa hai cặp cạnh ấy bằng nhau thì nó sẽ đồng dạng.

Cách 4: Chứng minh trường hợp cạnh-cạnh-cạnh: Nếu 3 cạnh của tam giác này tỉ lệ thuận với 3 cạnh của tam giác kia thì 2 tam giác này đồng dạng.

Cách 5: Chứng minh cạnh-góc-cạnh: Nếu 2 cạnh của tam giác này tỷ lệ với 2 cạnh của tam giác kia và 2 góc tạo bởi tạo các cặp cạnh đó bằng nhau thì 2 tam đó sẽ đồng dạng.

Các cách chứng minh hai tam giác đồng dạng – Bài tập về tam giác đồng dạng

Cách chứng minh 2 tam giác đồng dạng – hệ thức

Bài toán: Cho △ABC(AB<AC), AD là đường phân giác trong. Miền ngoài △ vẽ tia Cx sao cho góc BCx = góc BAD. Gọi I là giao điểm của Cx và AD. Chứng minh rằng:

1. a) △ADB∼△CDI

2. b) AD.AC=AB.AI

3. c) AD2 = AB.AC – BD.DC

Giải: Ta có hình vẽ:

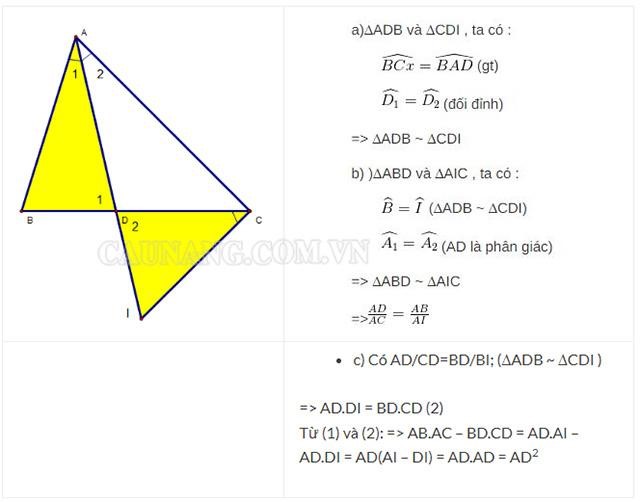
Chứng minh hai tam giác đồng dạng – Định lí Talet và hai đường thẳng song song

Bài toán: Cho tam giác ABC nhọn, đường cao BD và CE. Kẻ các đường cao DF và EG của  ∆ADE. Chứng minh:

1. a) △ADB∼△AEG

2. b) AD.AE = AB.AG = AC.AF

3. c) FG // BC

Giải: Ta có hình vẽ:

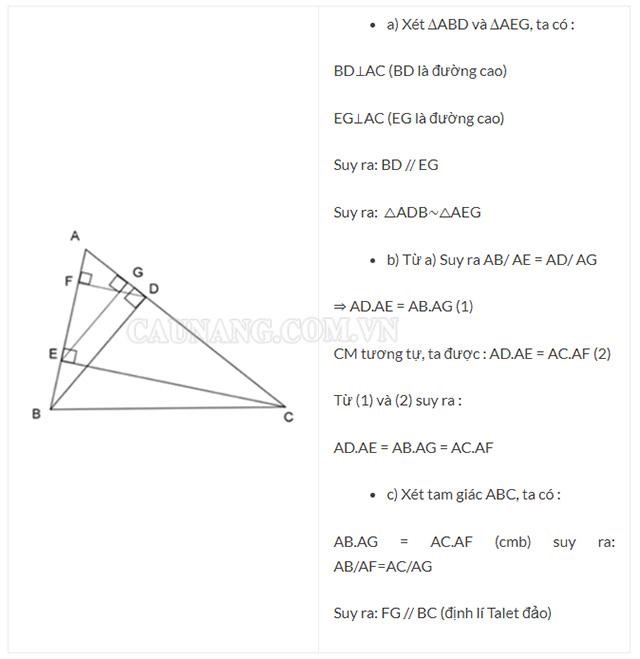
Chứng minh hai tam giác đồng dạng – góc tương ứng bằng nhau

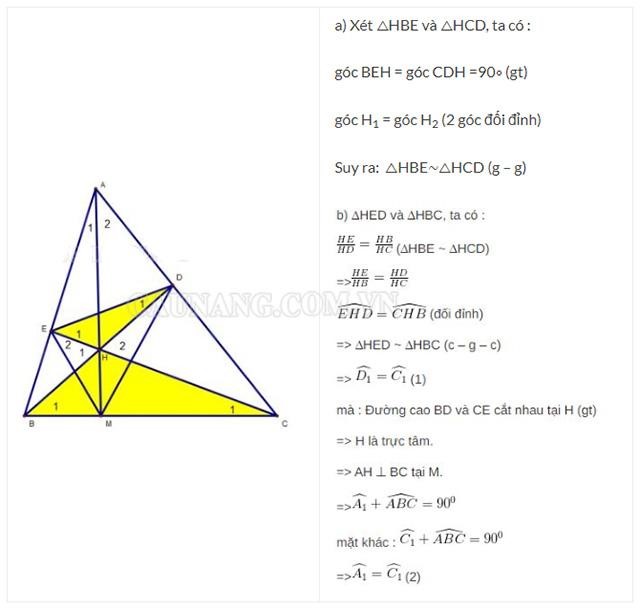
Bài toán: Cho △ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh:

1. a) △HBE∼△HCE

2. b) △HED∼△HBC và góc HDE = góc HAE

Giải: Ta có hình vẽ

Mong rằng các thông tin có trong bài viết trên đây đã giúp bạn hiểu thêm về 2 tam giác đồng dạng. Hãy truy cập website caunang.com.vn để tìm hiểu nhiều thông tin hữu ích khác.