Implementing VGG Neural Networks

In the last two articles, we went through implementing VGG11 neural network from scratch using PyTorch and also training it on the MNIST dataset. In this tutorial, we will be implementing all VGG neural networks in a generalized manner using PyTorch.

• Two weeks ago (part one): Implementing VGG11 from scratch using PyTorch.
• Last week (part two): Training our implemented VGG11 model from scratch using PyTorch.
• This week (part three): Implementing all the VGG models in a generalized manner using the PyTorch deep learning framework.

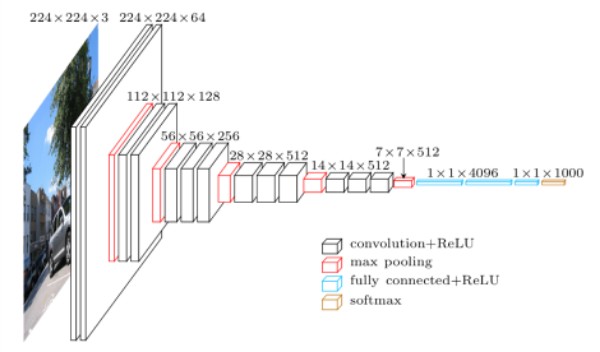Figure 1. Diagram showing architecture of the VGG neural network (Source.)

What will we be covering in this tutorial?

• Having a high-level understanding of VGG neural network architectures like VGG11, VGG13, VGG16, and VGG19.
• Getting to know which architectures we will implement.
• Getting into the coding part and implementing VGG neural networks using PyTorch.

In the rest of the tutorial, we will discuss all the technical details and try to understand the concepts clearly.

The VGG Neural Networks

The VGG neural networks were introduced in the paper Very Deep Convolutional Networks for Large-Scale Image Recognition by Karen Simonyan and Andrew Zisserman.

They published their paper and results in 2014. The team also secured first and second place in the ImageNet Challenge 2014 for localization and classification tasks respectively. This means that the VGG networks were some of the best convolutional neural networks in 2014 (probably the best in terms of accuracy). This led to many groundbreaking publications and findings in the field of convolutional neural networks in deep learning in the upcoming years.

We will not go through too many historical details of the paper here. We will focus on the network architectures mostly. The paper is very readable and you should probably give it a try as well. I am sure that you will enjoy it.

Further on, let us shift our attention to the different VGG neural network architectures as per the paper.

Different Architectures of the VGG Neural Network

The authors mentioned a total of 6 different VGG architectures in the paper.

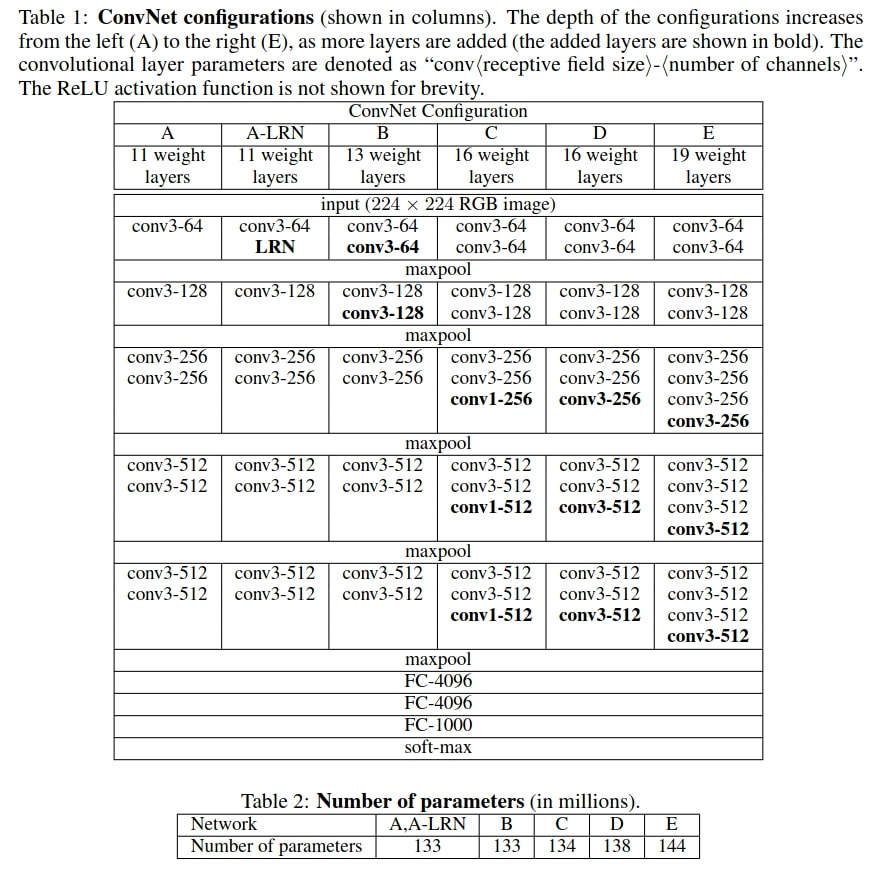Figure 2. Table showing all the VGG11 neural network architectures (Source).

Figure 2 shows Table 1 and Table 2 from the paper which consists of 6 different neural network configurations. They are A, A-LRN, B, C, D, and E. We will focus on configuration A, B, D, and E in this tutorial as they are the most commonly used ones.

Each of A, B, D, and E have 11, 13, 16, and 19 weight layers respectively. As such, we can call them VGG11, VGG13, VGG16, and VGG19.

We can also see that each of the architectures have Max Pooling operations after certain convolutional layers. Not to mention that we need to apply the ReLU activation after each convolutional layer as well. It has been skipped in the table just to make it easier to read.

One other thing to note here is that all the architectures have three fully connected layers. The first two fully connected layers have 4096 output features. The last fully connected layer is the final output layer with 1000 output features. This corresponds to the 1000 classes in the ImageNet dataset.

In figure 2, we can also see Table 2 which mentions the number of parameters each VGG network has. Starting from 133 million parameters for VGG11, the number goes to 144 million parameters for VGG19. We need to take note of these numbers. This is because we will be comparing the number parameters in our implemented networks with the above numbers later on. This should provide us with a good sanity check that our implementation is correct.

And just for reference, the following is the block diagram of VGG 11 network.

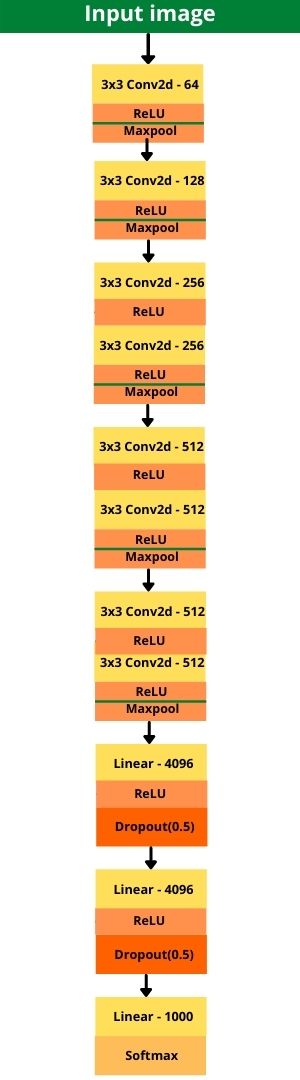Figure 3. Diagram showing the different layers of the VGG11 neural network model.

This should provide us with ample information to be able to implement all the VGG neural networks using PyTorch.

The PyTorch Version

For this tutorial, I have used PyTorch version 1.8.0. Although, we will be using some of the very core features of PyTorch only, still, updating your PyTorch version will ensure that you do not run into any unseen errors.

You can update your PyTorch version from here. Choose the command according to your system configuration and you are good to go.

Be sure to use a separate Python virtual environment or Anaconda environment (whichever you use) to install the latest versions of PyTorch. This ensures that you do not break any of your existing projects and there are no conflicts with the existing versions as well.

For the directory structure, we do not need anything strict for this tutorial. Just ensure that you name the directory appropriately and create a Python file to write the code.

Finally, we have set up everything we need for implementing VGG neural networks using PyTorch. Now we can get started with the coding.

Implementing VGG Neural Networks using PyTorch

We will write all the code in a single Python script. Let us call that script vgg_models.py. You can give any other relevant name as well.

As always, the following are the imports that we will need along the way.

import torch
import torch.nn as nn

We only need the torch module and torch.nn module for writing the code for the VGG neural network architectures.

VGG Configurations

Here, we will define the four VGG configurations that we discussed above. We will define a simple dictionary defining all the configurations names as keys and the configuration data as values.

# VGG configurations according to Table 1 in the paper
# https://arxiv.org/pdf/1409.1556v6.pdf
# configurations A (VGG11), B (VGG13), D (VGG16), and E (VGG19)
vgg_cfgs = {
    'A': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
    'B': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
    'D': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
    'E': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}

Going over the above code block.

• We have a vgg_cfgs dictionary where configuration names A, B, C, and D are the keys. The lists that they contain are the values and define all convolution and max-pooling operations of the network architectures. The numbers (64, 128, …) are the output channels of each of the convolutional layers. And 'M' indicates the max-pooling operations.
• Configuration A corresponds to the VGG11 model with 11 weight layers. If you take a look at figure 2, then you will be able to notice that we have defined the convolutional output channels and the max-pooling operations just as in the paper. It has 8 convolutional layers and 5 max-pooling operations.
• The other configurations are also according to the paper only. Configuration B corresponds to VGG13, C corresponds to VGG16, and D corresponds to VGG19. Taking a look at Table 2 in the paper will clear things out even more. You can always cross-check that we have defined all the layers correctly.

Also, you can notice in figure 2 that all the convolutional layers for configurations A, B, C, and D have 3×3 size kernels. This means that we can define the convolutional layers in a very generalized way.

One questions may arise here, “why not define the fully connected layers here as well?”. Well, all the VGG neural network configurations contain the same number of fully connected layers, that is three. The first two with 4096 output features, and the last classification head with 1000 output features. It will be much cleaner to define a single sequential block later rather than including those layers here, which might affect the simplicity of the configuration dictionary.

A Few Things to Note Before Moving Further

There are few things we need to keep in our mind before we go for the rest of the coding part.

• When the paper was published, the authors did not mention or use Batch Normalization in their neural network layers. This was simply because, the Batch Normalization paper was published a few months later by Sergey Ioffe and Christian Szegedy. This helps to deal with the issues of vanishing gradients while training very deep neural networks.
• Later implementations of the VGG neural networks included the Batch Normalization layers as well. Even the official PyTorch models have VGG nets with batch norm implemented.
• So, we will also include the batch norm layers at the required positions in the network. We will see to that while coding the layers.
• One other thing is the use of dropout after the first two fully connected layers. Although not mentioned in Table 2, the authors used dropout with a probability of 0.5 after the first two fully connected layers. You can find this information in the Training section of the paper. Therefore, we will also be using dropout after the first two fully connected layers.

The above are some points we need to keep in mind before coding the actual VGG network using PyTorch.

The Network Architecture Class

In this section, we will write a Python class to define the VGG neural network architectures in a generalized manner. We will call this class as VGG.

Let us write the whole class code first, then we will get into the detailed explanation of the code.

# VGG neural network class
class VGG(nn.Module):
    def __init__(self, in_channels=3, num_classes=1000, 
                 config=vgg_cfgs['A']):
        super(VGG, self).__init__()
        self.in_channels = in_channels
        self.num_classes = num_classes
        self.config = config

        # select convolutional layer configuration for the VGG net
        self.covolutional_layers = self.make_conv_layers(self.config)

        self.fully_connected = nn.Sequential(
            nn.Linear(512*7*7, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, num_classes)
        )

    # function to create the convolutional layers as per the selected config
    def make_conv_layers(self, config):
        layers = []
        in_channels = self.in_channels
        for op in config:
            if op == 'M':
                layers += [nn.MaxPool2d(kernel_size=2, stride=1)]
            else:
                layers += [
                           nn.Conv2d(in_channels=in_channels, 
                                      out_channels=op, kernel_size=3, 
                                      padding=1),
                           nn.BatchNorm2d(op),
                           nn.ReLU()
                ]
                in_channels = op
        return nn.Sequential(*layers)

    # the forward pass
    def forward(self, x):
        x = self.convolutional_layers(x)
        # flatten to prepare for the fully connected layers
        x = x.view(x.size(0), -1)
        x = self.fully_connected(x)
        return x

If you observe closely, then this code is shorter than implementing a single VGG11 class. At first sight, it might seem a bit complicated, but it’s quite easy to understand.

Let us go over the code.

The __init__() Method

• The __init__() method is accepting three parameters. They are in_channels, num_classes, and config. They have default values as 3, 1000, and vgg_cfgs['A'].
• The config parameter defines which VGG neural network architecture we want. It is VGG11 by default.
• After that, we initialize the variables in the __init__() method from lines 17 to 19.
• At line 22, we initialize the self.covolutional_layers by calling the make_conv_layers() function which we have defined at a later part. We will get to this shortly. Basically, this will populate the self.convolutional_layers with all the layers and operations that we define in the make_conv_layers() function.
• Starting from line 24, we have all the Linear layers inside a Sequential block. As discussed, there are three linear layers in total. The first two are followed by Dropout and ReLU activation. And the last one has 1000 output features.

The make_conv_layers() Method

This is the method where we will define all out convolutional layers, along with defining batch norm and max-pooling wherever needed. This accepts only one parameter, that is, config (the network configuration).

• At line 36, we define a list layers. This will hold all the Conv2d-BatchNorm2d-ReLU blocks and also the MaxPool2d layers.
• Line 37 initializes the input channels for the current model. We need to pass this information to the Conv2d layers.
• Now, we need to keep in mind that config is a list containing all the layer information. For example for config=vgg_cfgs['A'], it will hold [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M']. So, it is a list we can iterate through.
• This is exactly what we start doing at line 38. We iterate over all the operations in the list.
• At line 39, we check whether the operation is 'M', that is max-pooling. If that is the case, then we append a 2D max-pooling operations to layers.
• If the operation is not max-pooling, then it has to be any of the other numbers indicating the output channels for 2D convolutional layers. For this case, we append a stacking of Conv2d, BatchNorm2d, and ReLU to the layers.
• For the Conv2d layer, the input channels is in_channels which we update after every Conv2d-BatchNorm2d-ReLU operation. The output channels is op, kernel size is 3×3 and padding is 1.
• Finally, we return all the layers in a Sequential manner (line 50).

The forward() Method

The forward() method is pretty simple.

• At line 54, we pass all the data (tensors) through the convolutional_layers which provides us with the feature maps.
• Then we flatten all the feature maps at line 56 and pass them through the fully connected layers at line 57 to get the final output.
• And then we return the output.

The completes our VGG model class code. And one interesting thing is that we just implemented four different VGG neural networks in this generalized manner. We just need to provide the correct configuration while initializing the model and the VGG class will take care of the rest.

One final thing that is left is initializing the four VGG neural networks and printing the number of parameters. This will ensure that we have implemented everything correctly.

if __name__ == '__main__':
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    config_keys = list(vgg_cfgs.keys())
    for i, config in enumerate(config_keys):
        model = VGG(in_channels=3, num_classes=1000, config=vgg_cfgs[config]).to(device)
        print(f"Config: {config}, {model}")
        # total parameters in the model
        total_params = sum(p.numel() for p in model.parameters())
        print(f"[INFO]: {total_params:,} total parameters. \n")

• At line 60, we define the computation device. It does not matter much whether we use a CPU or GPU as we are not training any models here.
• Then we extract all the keys from vgg_cfgs dictionary and store them as a list in config_keys.
• From line 62, we start looping over the keys.
• At line 63, we initialize the VGG model using the current configuration key.
• After that, we print the entire model and also the number of parameters it has.

The output is going to be a long one, but it will provide us with all the model’s information.

Executing vgg_models.py for Implementing VGG Neural Networks using PyTorch

Finally, we have reached the point where can execute our Python script and check whether everything is running as expected or not.

Within your project directory, type the following command line your terminal/command line.

python vgg_models.py

You should get the following output.

Config: A, VGG(
  (covolutional_layers): Sequential(
    (0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU()
    (3): MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1, ceil_mode=False)
    (4): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (5): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (6): ReLU()
    (7): MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1, ceil_mode=False)
    (8): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (9): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (10): ReLU()
    (11): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (12): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (13): ReLU()
    (14): MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1, ceil_mode=False)
    (15): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (16): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (17): ReLU()
    (18): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (19): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (20): ReLU()
    (21): MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1, ceil_mode=False)
    (22): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (23): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (24): ReLU()
    (25): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (26): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (27): ReLU()
    (28): MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1, ceil_mode=False)
  )
  (fully_connected): Sequential(
    (0): Linear(in_features=25088, out_features=4096, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.5, inplace=False)
    (3): Linear(in_features=4096, out_features=4096, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.5, inplace=False)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)
[INFO]: 132,868,840 total parameters. 

Config: B, VGG(
  (covolutional_layers): Sequential(
    (0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU()
    (3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (5): ReLU()
    ...
  )
  (fully_connected): Sequential(
    (0): Linear(in_features=25088, out_features=4096, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.5, inplace=False)
    (3): Linear(in_features=4096, out_features=4096, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.5, inplace=False)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)
[INFO]: 133,053,736 total parameters. 

Config: D, VGG(
  (covolutional_layers): Sequential(
    (0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU()
    (3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (5): ReLU()
    ...
  )
  (fully_connected): Sequential(
    (0): Linear(in_features=25088, out_features=4096, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.5, inplace=False)
    (3): Linear(in_features=4096, out_features=4096, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.5, inplace=False)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)
[INFO]: 138,365,992 total parameters. 

Config: E, VGG(
  (covolutional_layers): Sequential(
    (0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU()
    (3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (5): ReLU()
    ...
  )
  (fully_connected): Sequential(
    (0): Linear(in_features=25088, out_features=4096, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.5, inplace=False)
    (3): Linear(in_features=4096, out_features=4096, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.5, inplace=False)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)
[INFO]: 143,678,248 total parameters.

After the first VGG network architecture, the above block shows truncated outputs for VGG13, VGG16, and VGG19 to ensure that things easy to read and understand.

We can see that for VGG11 we have 132,868,840 total parameters. For VGG13 it is 133,053,736 total parameters. For VGG16, the number of parameters is 138,365,992. And for VGG19, the number of parameters is 143,678,248.

We are getting the total number of parameters as expected. Although for VGG19, the total number of parameters is not exactly 144 million. It is very near to that. Still, this is the correct number.

This completes our implementation of four different VGG neural networks using PyTorch. Now, you can use your own class to initialize VGG models and train them on whichever dataset you wish. Quick note: these are not pre-trained.

Let others know in the comment section if you use this code in any of your small projects or to train a dataset.

Summary and Conclusion

In this tutorial, we learned how to implement four different VGG neural network architectures in a generalized manner using PyTorch. We went through the architectures from the paper in brief and then wrote our own PyTorch code for implementation. I hope that you learned something new from this tutorial.

If you have any doubts, thoughts, or suggestions, then please leave them in the comment section. I will surely address them.

You can contact me using the Contact section. You can also find me on LinkedIn, and Twitter.