How to Create a Simple Neural Network in Python – KDnuggets

The best way to understand how neural networks work is to create one yourself. This article will demonstrate how to do just that.

By Dr. Michael J. Garbade

Neural networks (NN), also called artificial neural networks (ANN) are a subset of learning algorithms within the machine learning field that are loosely based on the concept of biological neural networks.

Andrey Bulezyuk, who is a German-based machine learning specialist with more than five years of experience, says that “neural networks are revolutionizing machine learning because they are capable of efficiently modeling sophisticated abstractions across an extensive range of disciplines and industries.”

Basically, an ANN comprises of the following components:

• An input layer that receives data and pass it on
• A hidden layer
• An output layer
• Weights between the layers
• A deliberate activation function for every hidden layer. In this simple neural network Python tutorial, we’ll employ the Sigmoid activation function.

There are several types of neural networks. In this project, we are going to create the feed-forward or perception neural networks. This type of ANN relays data directly from the front to the back.

Training the feed-forward neurons often need back-propagation, which provides the network with corresponding set of inputs and outputs. When the input data is transmitted into the neuron, it is processed, and an output is generated.

Here is a diagram that shows the structure of a simple neural network:

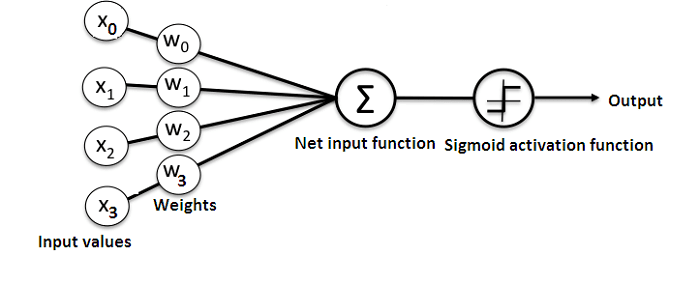
And, the best way to understand how neural networks work is to learn how to build one from scratch (without using any library).

In this article, we’ll demonstrate how to use the Python programming language to create a simple neural network.

The problem

Here is a table that shows the problem.

Input

Output

Training data 1
0
0
1
0

Training data 2
1
1
1
1

Training data 3
1
0
1
1

Training data 4
0
1
1
0

New Situation
1
0
0
?

We are going to train the neural network such that it can predict the correct output value when provided with a new set of data.

As you can see on the table, the value of the output is always equal to the first value in the input section. Therefore, we expect the value of the output (?) to be 1.

Let’s see if we can use some Python code to give the same result (You can peruse the code for this project at the end of this article before continuing with the reading).

Creating a NeuralNetwork Class

We’ll create a NeuralNetwork class in Python to train the neuron to give an accurate prediction. The class will also have other helper functions.

Even though we’ll not use a neural network library for this simple neural network example, we’ll import the numpy library to assist with the calculations.

The library comes with the following four important methods:

1. exp—for generating the natural exponential
2. array—for generating a matrix
3. dot—for multiplying matrices
4. random—for generating random numbers. Note that we’ll seed the random numbers to ensure their efficient distribution.

• Applying the Sigmoid function

We’ll use the Sigmoid function, which draws a characteristic “S”-shaped curve, as an activation function to the neural network.

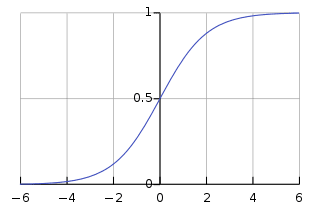
This function can map any value to a value from 0 to 1. It will assist us to normalize the weighted sum of the inputs.

Thereafter, we’ll create the derivative of the Sigmoid function to help in computing the essential adjustments to the weights.

The output of a Sigmoid function can be employed to generate its derivative. For example, if the output variable is “x”, then its derivative will be x * (1-x).

• Training the model

This is the stage where we’ll teach the neural network to make an accurate prediction. Every input will have a weight—either positive or negative.

This implies that an input having a big number of positive weight or a big number of negative weight will influence the resulting output more.

Remember that we initially began by allocating every weight to a random number.

Here is the procedure for the training process we used in this neural network example problem:

1. We took the inputs from the training dataset, performed some adjustments based on their weights, and siphoned them via a method that computed the output of the ANN.
2. We computed the back-propagated error rate. In this case, it is the difference between neuron’s predicted output and the expected output of the training dataset.
3. Based on the extent of the error got, we performed some minor weight adjustments using the Error Weighted Derivative formula.
4. We iterated this process an arbitrary number of 15,000 times. In every iteration, the whole training set is processed simultaneously.

We used the “.T” function for transposing the matrix from horizontal position to vertical position. Therefore, the numbers will be stored this way:

Ultimately, the weights of the neuron will be optimized for the provided training data. Consequently, if the neuron is made to think about a new situation, which is the same as the previous one, it could make an accurate prediction. This is how back-propagation takes place.

Wrapping up

Finally, we initialized the NeuralNetwork class and ran the code.

Here is the entire code for this how to make a neural network in Python project:

 
import
 numpy 
as
 np

class
 
NeuralNetwork
():
    
    
def
 __init__(
self
):
        
# seeding for random number generation
        np.random.seed(
1
)
        
        
#converting weights to a 3 by 1 matrix with values from -1 to 1 and mean of 0
        
self
.synaptic_weights = 
2
 * np.random.random((
3
, 
1
)) - 1

    
def
 sigmoid(
self
, x):
        
#applying the sigmoid function
        
return
 
1
 / (
1
 + np.exp(-x))

    
def
 sigmoid_derivative(
self
, x):
        
#computing derivative to the Sigmoid function
        
return
 x * (
1
 - x)

    
def
 train(
self
, training_inputs, training_outputs, training_iterations):
        
        
#training the model to make accurate predictions while adjusting weights continually
        
for
 iteration 
in
 range(training_iterations):
            
#siphon the training data via  the neuron
            output = 
self
.think(training_inputs)

            
#computing error rate for back-propagation
            error = training_outputs - output
            
            
#performing weight adjustments
            adjustments = np.dot(training_inputs.T, error * 
self
.sigmoid_derivative(output))

            
self
.synaptic_weights += adjustments

    
def
 think(
self
, inputs):
        
#passing the inputs via the neuron to get output
   
        
#converting values to floats
        
        inputs = inputs.astype(
float
)
        output = 
self
.sigmoid(np.dot(inputs, 
self
.synaptic_weights))
        
return
 output


if
 __name__ == 
"__main__"
:

    
#initializing the neuron class
    neural_network = 
NeuralNetwork
()

    
print
(
"Beginning Randomly Generated Weights: "
)
    
print
(neural_network.synaptic_weights)

    
#training data consisting of 4 examples--3 input values and 1 output
    training_inputs = np.array([[
0
,
0
,
1
],
                                [
1
,
1
,
1
],
                                [
1
,
0
,
1
],
                                [
0
,
1
,
1
]])

    training_outputs = np.array([[
0
,
1
,
1
,
0
]]).T

    
#training taking place
    neural_network.train(training_inputs, training_outputs, 
15000
)

    
print
(
"Ending Weights After Training: "
)
    
print
(neural_network.synaptic_weights)

    user_input_one = str(input(
"User Input One: "
))
    user_input_two = str(input(
"User Input Two: "
))
    user_input_three = str(input(
"User Input Three: "
))
    
    
print
(
"Considering New Situation: "
, user_input_one, user_input_two, user_input_three)
    
print
(
"New Output data: "
)
    
print
(neural_network.think(np.array([user_input_one, user_input_two, user_input_three])))
    
print
(
"Wow, we did it!"
)

Here is the output for running the code:

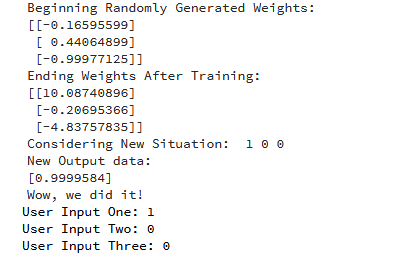
We managed to create a simple neural network.

The neuron began by allocating itself some random weights. Thereafter, it trained itself using the training examples.

Consequently, if it was presented with a new situation [1,0,0], it gave the value of 0.9999584.

You remember that the correct answer we wanted was 1?

Then, that’s very close—considering that the Sigmoid function outputs values between 0 and 1.

Of course, we only used one neuron network to carry out the simple task. What if we connected several thousands of these artificial neural networks together? Could we possibly mimic how the human mind works 100%?

Do you have any questions or comments?

Please provide them below.

Bio: Dr. Michael J. Garbade is the founder and CEO of Los Angeles-based blockchain education company LiveEdu . It’s the world’s leading platform that equips people with practical skills on creating complete products in future technological fields, including machine learning.

Related: