Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?

4.1

/

5

(

90

bình chọn

)

Hình lăng trụ trong hình học không gian không còn xa lạ gì đối với mọi người rồi. Nhưng liệu bạn có biết hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng không? Hẳn nhiều người không thể nắm rõ câu hỏi này. Để giúp bạn trả lời câu hỏi, chúng tôi sẽ giải đáp ở phần dưới đây. Và kèm theo đó là những thông tin quan trọng liên quan đến hình lăng trụ tam giác đều trong hình học không gian. Không những thế chúng tôi sẽ có những bài toán liên quan đến hình lăng trụ giúp bạn có thể học tốt hơn môn hình học không gian đặc biệt là những bài toán liên quan đến hình lăng trụ. Hãy cùng chúng tôi đọc lý bài viết này nhé. Đây sẽ là tài liệu tham khảo hữu ích dành cho thầy cô, phụ huynh và học sinh.

Trả lời câu hỏi hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng

Câu trả lời của câu hỏi này chính là 4 mặt phẳng đối xứng. Như chúng ta đã biết mặt phẳng đối xứng tức là với hai hình khối A và A’, một mặt phẳng (m). A và A’ là hình chiếu của nhau qua (m). Chúng ta có thể hiểu rằng, mặt phẳng (m) cắt một hình thành hai hình bằng nhau là A và A’ . Có 4 mặt phẳng đối xứng trong một hình lăng trụ tam giác đều. Để dễ hình dung các bạn nên vẽ hình ra. Mặt phẳng đầu tiên đó là mặt phẳng được tạo bởi trung điểm ba cạnh bên. Còn ba mặt phẳng còn lại chính là mặt phẳng được tạo bởi một cạnh và trung điểm của hai cạnh còn lại. Như vậy, chúng ta có 4 mặt phẳng đối xứng.

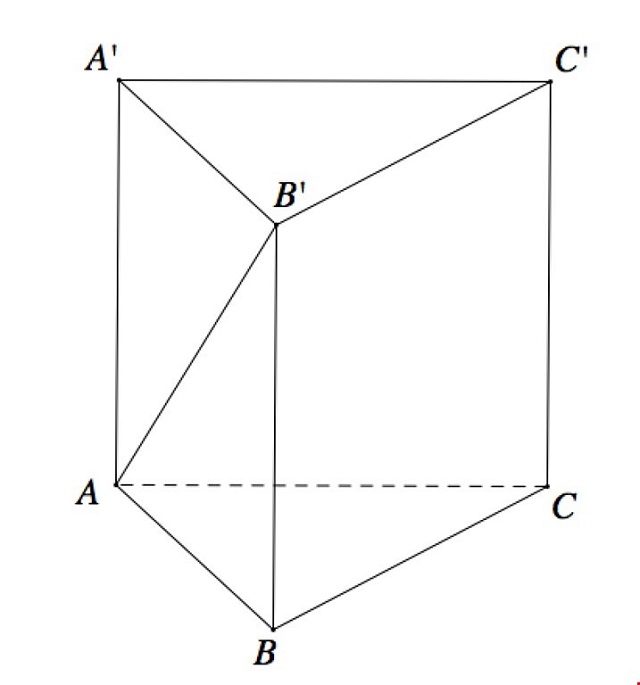
Tính chất của hình lăng trụ tam giác đều mà bạn nên nắm rõ

Ngoài trả lời câu hỏi về hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng  thì chúng tôi sẽ cung cấp cho bạn một số thông tin, tính chất của một hình lăng trụ. Hình lăng trụ là một khối đa diện có hai đáy là đa giác và hai mặt đáy bằng nhau và song song với nhau. Các mặt bên của hình trụ là hình bình hành, cạnh bên thì song song và bằng nhau. Hình lăng trụ đều là hình lăng trụ mà hai đáy là các đa giác đều. Có rất nhiều loại lăng trụ đều thường gặp đó là lăng trụ tam giác đều, lăng trụ tứ giác đều, lăng trụ ngũ giác đều,… Khi đó lăng trụ tam giác đều là hình lăng trụ đứng có đáy là tam giác đều. Lăng trụ tam giác đều có tính chất là hai đáy là hai tam giác bằng nhau và là hai tam giác đều. Các cạnh bên vuông góc với mặt đáy. Các mặt bên là hình chữ nhật. Thể tích của hình lăng trụ sẽ được tính theo công thức sau : V= B*h (sẽ bằng diện tích của mặt đáy nhân với khoảng cách giữa hai đáy có thể gọi là chiều cao của hình lăng trụ).

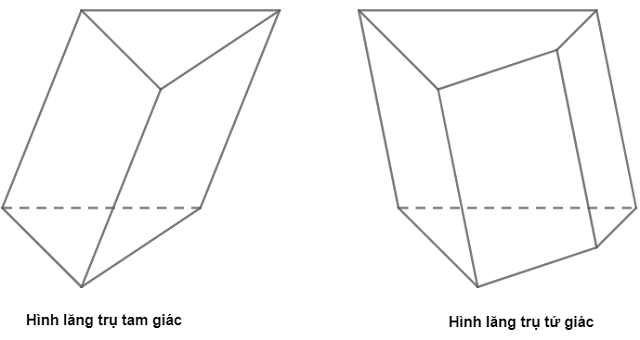
Một số bài tập liên quan đến lăng trụ tam giác đều bạn nên chú ý

Sau đây là một số bài toán liên quan đến hình lăng trụ có thể giúp bạn nhớ những kiến thức lý thuyết vừa mới học xong.

Bài tập 1 : Bạn hãy chọn một đáp án đúng nhất trong các câu trả lời sau.

Bạn hãy cho biết các mặt bên của một hình bát diện đều là hình gì ?

1. Hình tam giác cân
2. Hình vuông
3. Hình tam giác đều
4. Hình chữ nhật

Bài tập 2 : Cho hình lăng trụ tam giác MNO.M ‘N’O’ với mặt đáy là một tam giác với góc M=90 Độ, Cạnh MN=2, NO=3, cạnh bên M’M = 4. Bạn hãy tính thể tích của hình lăng trụ này.

Bài tập 3 : Cho các mệnh đều như sau, hãy nhận xét mệnh đề nào đúng, mệnh đề nào sai.

1. Hai đa diện bằng nhau là hai khối đa diện đều có thể tích bằng nhau
2. Hai khối đa diện có thể tích bằng nhau thì hai khối đa diện đó bằng nhau
3. Khi hai hình lập phương có thể tích bằng nhau thì hai hình lập phương đó bằng nhau
4. Khi hai hình hộp chữ nhật có thể tích bằng nhau thì hai hình hộp chữ nhật đó bằng nhau

Trên đây là những dạng bài tập bạn có thể gặp khi học hình học không gian về hình lăng trụ, đặc biệt là lăng trụ đều. Bạn hãy làm thật kỹ những dạng toán này nhé, biết đâu nó sẽ giúp ích cho bạn qua những kỳ thi cuối kỳ hay là giữa kỳ.

Vậy, bây giờ bạn có thể trả lời chắc chắn câu hỏi hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng đáp án chính xác là 4 mặt phẳng đối xứng. Như vậy, với những thông tin trên của bài viết này chắc rằng bạn đã có những điều riêng để bỏ túi cho riêng mình rồi chứ. Với phần lý thuyết ở trên, bạn có  thể hoàn thành bài thi của mình để vượt qua kì thi của mình. Tuy nhiên hãy học kỹ phần lý thuyết trước khi làm bài tập. Và để làm tốt bài tập phần này thì bạn nên làm thật kỹ, thật nhiều dạng toán khác nhau để khi cần thiết, bạn chỉ cần đọc sơ qua đề là có thể giải quyết bài toán dạng này rồi. Hi vọng với bài viết này bạn sẽ có một kỳ thi thật tốt, điểm như mình mong muốn. Và điều cuối cùng đó là đừng quên để lại lời nhắn của mình ở phía dưới bài viết này nhé.