Giải vở bài tập toán 5 bài 172 : Luyện tập chung

Lựa chọn câu để xem lời giải nhanh hơn

Bài 1

Tính :

a) \((1,35:0,54 \times 4,2 – 5,5):\)\((7,2 – 4,7)\)

b) 2 giờ 55 phút + 17 giờ 20 phút : 8

Phương pháp giải:

– Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.

– Biểu thức có phép tính cộng, trừ, nhân, chia thì ta thực hiện tính phép nhân, chia trước, thực hiện phép cộng, trừ sau.

Lời giải chi tiết:

a) \((1,35:0,54 \times 4,2 – 5,5):\)\((7,2 – 4,7)\)

\(\eqalign{ &=\left( {2,5 \times 4,2 – 5,5} \right):2,5 \cr 
& = \left( {10,5 – 5,5} \right):2,5 \cr 
& = 5:2,5 \cr 
& = 2 \cr} \)

b) 2 giờ 55 phút + 17 giờ 20 phút : 8

    = 2 giờ 55 phút + 2 giờ 10 phút

    = 4 giờ 65 phút

    = 5 giờ 5 phút

Bài 2

Viết tiếp vào chỗ chấm cho thích hợp :

Số trung bình cộng của :

a) \(28 ; 34 ; 41 ; 45\) là: ………………………….

b) \(3,52 ; 0,71 ; 6,04 ; 5,12 ; 4,46\) là: ……

c)  \(\displaystyle {1 \over 2};{3 \over 4};{4 \over 5}\) là: ………………………………..

Phương pháp giải:

Áp dụng công thức : Số trung bình cộng = tổng : số các số hạng. 

Lời giải chi tiết:

Số trung bình cộng của :

a) \(28 ; 34 ; 41 ; 45\) là :

\((28 + 34 + 41 + 45) : 4 = 37\)

b) \(3,52 ; 0,71 ; 6,04 ; 5,12 ; 4,46\) là : 

\((3,52 + 0,71 + 6,04 + 5,12 + 4,46)\) \(: 5= 3,97\)

c) \(\displaystyle{1 \over 2};{3 \over 4};{4 \over 5}\) là : 

\(\displaystyle\left({1 \over 2}+{3 \over 4}+{4 \over 5}\right) : 3 = {{41} \over {60}}\) 

Bài 3

Một trường tiểu học có tỉ số phần trăm của số học sinh nữ và số học sinh nam là 112%. Biết rằng trường đó có 636 học sinh. Hỏi trường tiểu học đó có bao nhiêu học sinh nam ?

Phương pháp giải:

– Tìm tỉ số giữa số học sinh nữ và số học sinh nam

– Giải bài toán tìm hai số khi biết tổng và hiệu của hai số đó.

Lời giải chi tiết:

Vì tỉ số phần trăm của số học sinh nữ và số học sinh nam là 112% nên tỉ số của số học sinh nữ và số học sinh nam là  $\frac{{112}}{{100}} = \frac{{28}}{{25}}$

Tổng số phần bằng nhau là

28 + 25 = 53 (phần)

Số học sinh nam của trường đó là

636 : 53 x 25 = 300 (học sinh)

Đáp số : 300 học sinh.

Bài 4

Giá một áo sơ mi là 90 000 đồng . Sau hai lần giảm giá, mỗi lần giảm 10% (so với giá ban đầu) thì giá bán áo sơ mi đó là bao nhiêu đồng ?

Phương pháp giải:

– Tìm số tiền được giảm sau khi giảm giá lần đầu = giá bán ban đầu : 100 × 10.

– Tìm giá bán áo sơ mi sau giảm giá lần đầu 

– Tìm số tiền được giảm sau khi giảm giá lần thứ hai 

– Tìm giá bán áo sơ mi sau hai lần giảm giá 

Lời giải chi tiết:

Số tiền giảm giá mỗi áo sơ mi lần đầu là :

90000 : 100 ⨯ 10 = 9000 (đồng)

Giá bán áo sơ mi sau giảm giá lần đầu là :

90000 – 9000 = 81000 (đồng)

Số tiền giảm giá mỗi áo sơ mi lần thứ hai là :

81000 : 100 ⨯ 10 = 8100 (đồng)

Giá bán áo sơ mi sau hai lần giảm giá :

81000 – 8100 = 72900 (đồng)

                   Đáp số : 72900 đồng.

Bài 5

Một tàu thủy có vận tốc khi nước lặng là a km/giờ, vận tốc của dòng nước là b km/giờ.

a) Tính vận tốc của tàu thủy khi tàu xuôi dòng.

b) Tính vận tốc của tàu thủy khi tàu ngược dòng.

c) Dùng sơ đồ đoạn thẳng để biểu thị hiệu vận tốc của tàu thủy khi tàu xuôi dòng và khi tàu ngược dòng.

Phương pháp giải:

Áp dụng các công thức:

– Vận tốc xuôi dòng = vận tốc khi nước lặng + vận tốc dòng nước.

– Vận tốc ngược dòng = vận tốc khi nước lặng – vận tốc dòng nước.

Lời giải chi tiết:

a) Vận tốc của tàu thủy khi tàu xuôi dòng là :

a + b (km/giờ)

b) Vận tốc của tàu thủy khi tàu ngược dòng là :

a – b (km/giờ)

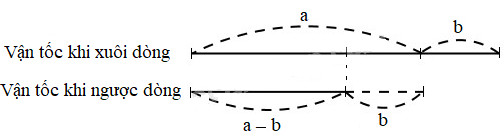
c) Ta có sơ đồ : 

Hiệu vận tốc của tàu thủy khi tàu xuôi dòng và khi tàu ngược dòng được thể hiện trên sơ đồ là đoạn thẳng b + b = b ⨯ 2

Vậy : Hiệu vận tốc của tàu thủy khi tàu xuôi dòng và khi tàu ngược dòng bằng 2 lần vận tốc của dòng nước.

Loigiaihay.com