Giải bài tập SGK toán 11 Phần Đại Số -Chương 4-Bài 2: Giới hạn của hàm số | Lớp học thêm toán | Trung tâm học toán | Trung tâm luyện thi toán
Để xem lời giải chi tiết SGK lớp 3,4,5,6,7,8,9,10,11,12 vui lòng truy cập website : edusmart.vn
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 123: Xét hàm số
1. Cho biến x những giá trị khác 1 lập thành dãy số xn, xn → 1 như trong bảng sau:
Khi đó, các giá trị tương ứng của hàm số
f(x1), f(x2),…, f(xn), …
cũng lập thành một dãy số mà ta kí hiệu là f(xn).
a) Chứng minh rằng f(xn) = 2xn = (2n + 2)/n.
b) Tìm giới hạn của dãy số f(xn).
2. Chứng minh rằng với dãy số bất kì xn, xn ≠ 1 và xn → 1, ta luôn có f(xn) → 2.
(Với tính chất thể hiện trong câu 2, ta nói hàm số 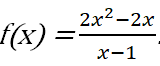
Lời giải:
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 127: Trong biểu thức (1) xác định hàm số y = f(x) ở Ví dụ 4, cần thay 2 bằng số nào để hàm số có giới hạn là -2 khi x → 1?
Lời giải:
cần thay 2 bằng 7 để hàm số có giới hạn là -2 khi x → 1
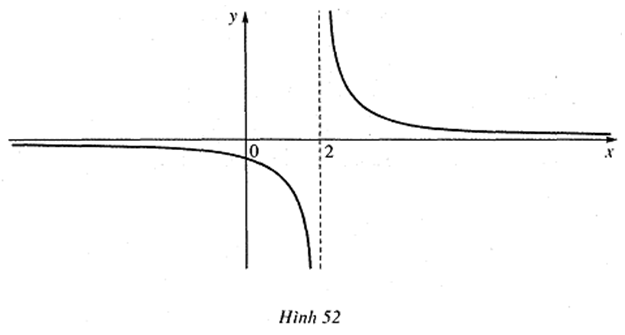
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 127: Cho hàm số f(x) = 1/(x-2) có đồ thị như ở Hình 52
Quan sát đồ thị và cho biết:
– Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào.
– Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Lời giải:
– Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị dương vô cực
– Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị âm vô cực
Bài 1 (trang 132 SGK Đại số 11): Dùng định nghĩa tìm các giới hạn sau:
Lời giải:
Bài 2 (trang 132 SGK Đại số 11):
Tính limun, limvn, limf(un), limf(vn).
Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0?
Lời giải:
Bài 3 (trang 132 SGK Đại số 11): Tính các giới hạn sau:
Lời giải:
Bài 4 (trang 132 SGK Đại số 11): Tìm các giới hạn sau :
Lời giải:
Bài 5 (trang 133 SGK Đại số 11): Cho hàm số f(x) = …
a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x →- ∞,x →3–,x →-3+
b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
Lời giải:
Bài 6 (trang 133 SGK Đại số 11): Tính:
Lời giải:
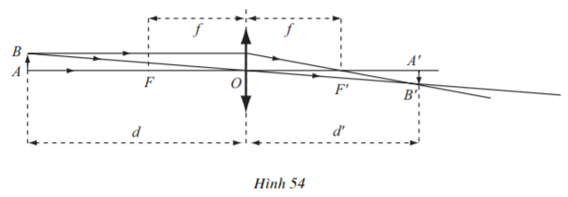
Bài 7 (trang 133 SGK Đại số 11): Một thấu kính hội tụ có tiêu cự là f. Gọi d và d‘ lần lượt là khoảng cách từ một vật thật AB và ảnh A‘B‘ của nó tới quang tâm O của thấu kính (hình dưới).
Lời giải:
Ý nghĩa: khi vật xa vô cực thì khoảng cách từ ảnh đến quang tâm bằng tiêu cực.

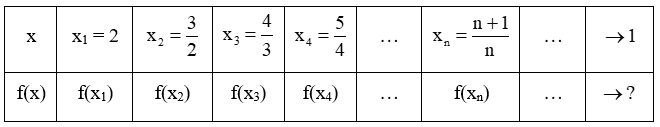

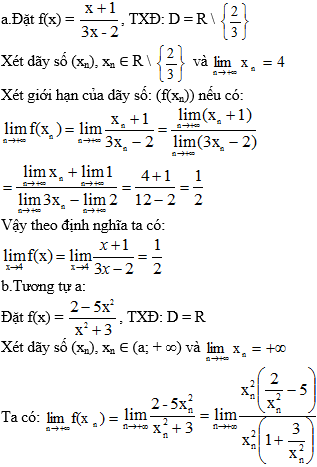

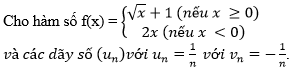

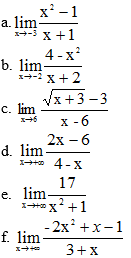
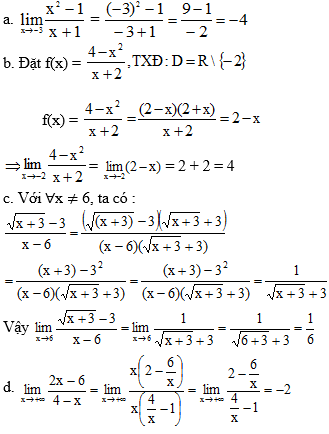

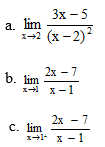

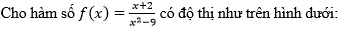

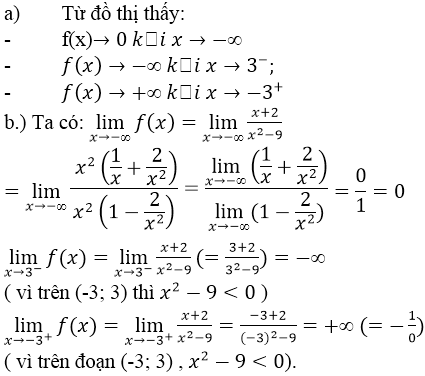
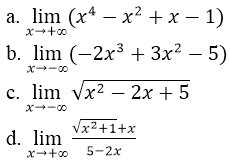
















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


