Giải bài 1,2,3,4,5,6,7 trang 44,45,46 Toán 9 tập 1: Nhắc lại và bổ sung các khái niệm về hàm số
Lý thuyết và Giải bài 1 trang 44; Bài 2,3,4,5,6 trang 45; bài 7 trang 46 SGK Toán Đại số 9 tập 1: Nhắc lại và bổ sung các khái niệm về hàm số – Chương 2 Hàm số bậc nhất.
A. Tóm tắt kiến thức Nhắc lại và bổ sung các khái niệm về hàm số:
1. Định nghĩa hàm số:
Nếu đại lượng y phụ thuộc vào một đâị lượng thay đổi sao cho với mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x được gọi là biến số.
Hàm số thường được kí hiệu bởi những chữ f, g, h… chẳng hạn khi y là một hàm số của biến số x, ta viết y = f(x) hoặc y = g(x),…
– f(a) là giá trị của hàm số y = f(x) tại x = a.
Khi hàm số y được cho bởi công thức y = f(x), muốn tính giá trị f(a) của hàm số tại x = a, ta thay x = a vào biểu thức f(x) rồi thực hiện các phép tính trong biểu thức.
– Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là một hàm hằng.
2. Đồ thị của hàm số:
Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số y = f(x).
3. Hàm số đồng biến, hàm số nghich biến:
Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc tập số thực R. Với x1, x2 túy ý thuộc R:
a) Nếu x1< x2 mà f(x1 ) < f(x2 ) thì hàm số được gọi là hàm đồng biến.
b) Nếu x1< x2 mà f(x1 ) > f(x2 ) thì hàm số được gọi là hàm nghịch biến.
B. Hướng dẫn giải bài tập trang 44, 45 SGK Toán đại số 9 tập 1
Bài 1 trang 44
a) Cho hàm số y = f(x) = 2/3x.
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3).
b) Cho hàm số y = g(x) =2/3x + 3.
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3).
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lầy cùng một giá trị ?
hướng dẫn giải bài 1:
a) Hàm số y = f(x) = 2/3x
f(-2) = 2/3(-2) = -4/3; f(-1) = -2/3; f(0) = 0; f(1/2) = 1/3; f(1) = 2/3; f(2) = 4/3; f(3) = 2.
b) Hàm số y = g(x) =2/3x + 3
g(-2) =5/3; g(-1) =7/3; g(0) = 3; g(1/2) = 10/3; g(1) = 11/3; g(2) = 13/3; g(3) = 5.
c) Khi x lấy cùng một giá trị thì giá trị của g(x) lớn hơn giá trị của f(x) là 3 đơn vị.
Bài 2 trang 45
Cho hàm số y = -1/2x + 3.
Quảng cáo
a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:
x
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
y=-1/2x + 3
b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?
hướng dẫn giải bài 2:
Với y = -1/2x + 3, ta có
f(-2,5) = -1/2(-2,5) + 3 = (2,5 + 6)/2 = 4,25;
Tương tự: f(-2) = 4; f(-1,5) = 3,75 ; f(-1) = 3,5 ; f(-0,5) = 3,25; f(0) = 3; f(0,5) = 2,75; f(1) = 2,5 ; f(1,5) = 2,25 ; f(2) = 2 ; f(2,5) = 1,75.
Điền vào bảng ta được
x
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
y=-1/2x + 3
4,25
4
3,75
3,5
3,25
3
2,75
2,5
2,25
2
1,75
Bài 3 trang 45
Cho hai hàm số y = 2x và y = -2x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?
hướng dẫn giải bài 3:

a) Đồ thị củahàm số y = 2x là đường thẳng đi qua O và điểm A(1; 2).
Đồ thị của hàm số y = -2x là đường thẳng đi qua O và điểm B(1; -2).
Quảng cáo
b) Hàm số y = 2x đồng biến vì khi x tăng lên thì y tương ứng tăng lên.
Hàm số y = -2x nghịch biến vì khi x tăng lên thì y tương ứng giảm đi.
y= 2x
-1
0
1
2
y =-2x
-2
0
2
4
y= -2x
2
0
-2
-4
Phần 2: Luyện tập Toán 9
Bài 4 trang 45
Đồ thị hàm số y = √3 x được vẽ bằng compa và thước thẳng ở hình 4.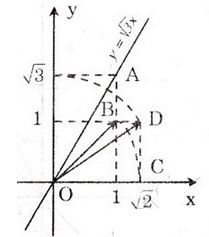
Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
hướng dẫn giải bài 4:
Ta biết rằng đồ thị hàm số y = √3 x là một đường thẳng đi qua gốc tọa độ. Hơn nữa, khi x = 1 thì y = √3. Do đó điểm A(1; √3) thuộc đồ thị. Vì thế để vẽ đồ thị này, ta phải xác định điểm A trên mặt phẳng tọa độ. Muốn vậy ta phải xác định điểm trên trục tung biểu diễn số √3. Ta có:

Hình vẽ trong SGK thể hiện OC = OB = √2 và theo định lí Py-ta-go![]()
Dùng compa ta xác định được điểm biểu diễn số √3. trên Oy. Từ đó xác định được điểm A.
Bài 5 trang 45
a) Vẽ đồ thị hàm số y = x và y =2x trên cùng một mặt phẳng tọa độ Oxy (h.5).

b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ Y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ của các điểm A, B và tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimét.
hướng dẫn giải bài 5:
Bài giải:
a) Xem hình bên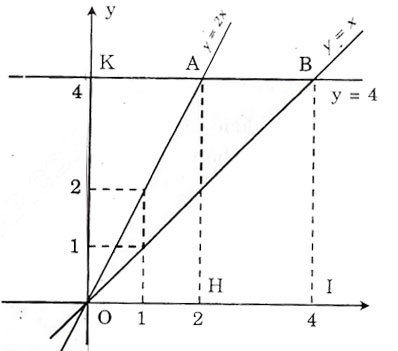
b) A(2; 4), B(4; 4).
Tính chu vi ∆OAB.

Bài 6 trang 45
Cho các hàm số y = 0,5x và y = 0,5x + 2
a) Tính giá trị y tương ứng với mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:
x
-2,5
-2,25
-1,5
-1
0
1
1,5
2,25
2,5
y= 0,5x
y = 0,5x + 2
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị ?
Đáp án và hướng dẫn giải bài 6:
a) Tính các giá trị của y ta được:
x
-2,5
-2,25
-1,5
-1
0
1
1,5
2,25
2,5
y= 0,5x
-1,25
-1,125
-0,75
-0,5
0
0,5
0,75
1,125
1,25
y = 0,5x + 2
0,75
0,875
1,25
1,5
2
2,5
2,75
3,125
3,25
Khi x lấy cùng một giá trị thì giá trị của hàm số y = 0,5x + 2 lớn hơn giá trị của hàm số y = 0,5x là 2 đơn vị.
Bài 7 trang 46 Toán 9 tập 1
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2 .
Hãy chứng minh f(x1 ) < f(x2 ) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
hướng dẫn giải bài 7:
Ứng với giá trị x1 thì hàm số nhận giá trị f(x1) = 3×1
Ứng với giá trị x2 thì hàm số nhận giá trị f(x2) = 3×2
Xét hiệu f(x1) – f(x2) = 3×1 – 3×2
- f(x1) – f(x2) = 3(x1 – x2) (1)
Theo giả thiết x1 < x2 nên x1 – x2 < 0 (2)
Từ (1) và (2) ta suy ra: f(x1) – f(x2) < 0 ó f(x1) < f(x2)
Vậy x1 < x2 => f(x1) < f(x2) (3)
Vì x1, x2 là hai số thực bất kì nên từ (3) ta kết luận hàm số y = 3x đồng biến trên tập số thứucj R vì (3) đúng với mọi giá trị bất kì cua x ∈ R.















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


