Giải bài 1, 2, 3 trang 43 SGK Giải tích 12

Bài 1 trang 43 sách sgk giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:

a) \(y{\rm{ }} = {\rm{ }}2{\rm{ }} + {\rm{ }}3x{\rm{ }}-{\rm{ }}{x^3}\) ;             b) \(y{\rm{ }} = {\rm{ }}{x^3} + {\rm{ }}4{x^2} + {\rm{ }}4x\);

c) \(y{\rm{ }} = {\rm{ }}{x^3} + {\rm{ }}{x^2} + {\rm{ }}9x\) ;            d) \(y{\rm{ }} = {\rm{ }}-2{x^3} + {\rm{ }}5\) ;

Giải:

Câu a:

Xét hàm số \(y{\rm{ }} = {\rm{ }}2{\rm{ }} + {\rm{ }}3x{\rm{ }}-{\rm{ }}{x^3}\)

Tập xác định: \(D=\mathbb{R}.\)

Sự biến thiên:

Đạo hàm: \(y’ = 3- 3x^2\) .

Ta có: \(y’ = 0 ⇔ x = ± 1\) .

Vậy hàm số đồng biến trên các khoảng \((-1;1)\), nghịch biến trên các khoảng \(\left( { – \infty ; – 1} \right)\) và \(\left( {1; + \infty } \right).\)

Cực trị: Hàm số đạt cực đại tại \(x=1\), giá trị cực đại

\(y\)CĐ=\(y(1)=4\), đạt cực tiểu tại \(x=-1\) và

\(y\)CT=\(y(-1)=0\).

Giới hạn: \(\mathop {\lim }\limits_{x \to – \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = – \infty\)

Bảng biến thiên:

         

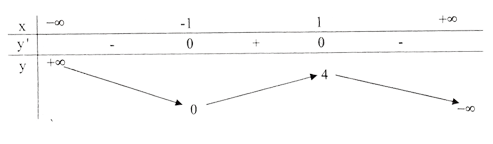
Đồ thị cắt trục \(Ox\) tại các điểm \((2;0)\) và \((-1;0)\), cắt \(Oy\) tại điểm \((0;2)\).

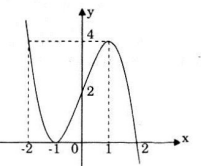
Đồ thị:

Ta có: \(y”=6x\); \(y”=0 ⇔ x=0\). Với \(x=0\) ta có \(y=2\). Vậy đồ thị hàm số nhận điểm \(I(0;2)\) làm tâm đối xứng.

Nhận thấy, nhánh bên trái vẫn còn thiếu một điểm để vẽ đồ thị, dựa vào tính đối xứng ta chọn điểm của hoành độ \(x=-2\) suy ra \(y=4\).

Câu b:

Xét hàm số \(y{\rm{ }} = {\rm{ }}{x^3} + {\rm{ }}4{x^2} + {\rm{ }}4x\)

Tập xác định: \(D=\mathbb{R}.\)

Sự biến thiên:

Đạo hàm: \(y’ = 3x^2+ 8x + 4\).

\(y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = – 2\\ x = – \frac{2}{3} \end{array} \right.\)

Hàm số đồng biến trên các khoảng \(\left( { – \infty ; – 2} \right)\) và \(\left( { – \frac{2}{3}; + \infty } \right)\) và nghịch biến trên \(\left( { – 2; – \frac{2}{3}} \right).\)

Cực trị:

Hàm số đạt cực đại tại \(x=-2\), giá trị cực đại \(y\)cđ = \(y(-2) = 0\).

Hàm số đạt cực tiểu tại \(x=-\frac{2}{3}\), giá trị cực tiểu \(y_{ct}=y\left ( -\frac{2}{3} \right )=-\frac{32}{27}.\)

Giới hạn: \(\mathop {\lim }\limits_{x \to – \infty } y = – \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\).

Bảng biến thiên:

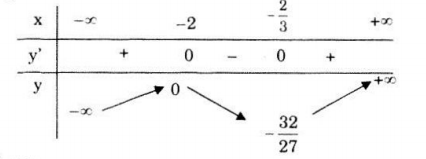
Đồ thị hàm số cắt trục \(Oy\) tại điểm \((0;0)\), cắt trục \(Ox\) tại điểm có hoành độ là nghiệm của phương trình: \({x^3} + 4{x^2} + 4x = 0⇔ x=0\) hoặc \(x=-2\) nên tọa độ các giao điểm là \((0;0)\) và \((-2;0)\).

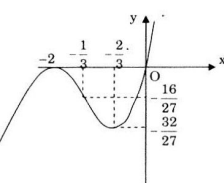
Đồ thị hàm số:

Tâm đối xứng của đồ thị hàm số: \(y”=6x+8;\)\(y”=0\Leftrightarrow x=-\frac{4}{3}\Rightarrow y=-\frac{16}{27}.\) 

Câu c:

Xét hàm số \(\small y = x^3 + x^2+ 9x\)

Tập xác định: \(D=\mathbb{R}.\)

Sự biến thiên:

Đạo hàm: \(y’ = 3x^2+ 2x + 9 > 0, ∀x\).

Vậy hàm số luôn đồng biến trên \(\mathbb{R}\) và không có cực trị.

Giới hạn: \(\mathop {\lim }\limits_{x \to – \infty } y = – \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\).

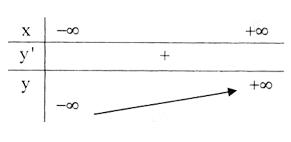
Bảng biến thiên :

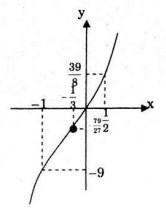
Đồ thị:

Đồ thị hàm số cắt trục \(Ox\) tại điểm \((0;0)\), cắt trục \(Oy\) tại điểm \((0;0)\).

Đồ thị hàm số có tâm đối xứng là điểm có hoành độ là nghiệm của phương trình \(y”=0 ⇔ 6x+2=0 ⇔\) \(x=-\frac{1}{3}.\) Suy ra tọa độ tâm đối xứng là: \(I\left ( -\frac{1}{3};-\frac{79}{27} \right ).\)

Lúc này ta vẫn chưa có đủ điểm để vẽ đồ thị hàm số, ta cần lấy thêm hai điểm có hoành độ cách đều hoành độ \(x_1\) và \(x_2\) sao cho \(\left| {{x_1} – \left( { – \frac{1}{3}} \right)} \right| = \left| {{x_2} – \left( { – \frac{1}{3}} \right)} \right|\), khi đó hai điểm này sẽ đối xứng nhau qua điểm uốn. Ta chọn các điểm \((-1;-9)\) và \(\left ( \frac{1}{2};\frac{39}{8} \right ).\)

Câu d:

Xét hàm số \(y=-2x^3+5\)

Tập xác định: \(D=\mathbb{R}.\)

Sự biến thiên:

Đạo hàm: \(y’ = -6x^2≤ 0, ∀x\).

Vậy hàm số luôn nghịch biến trên \(\mathbb R\).

Hàm số không có cực trị.

Giới hạn: \(\mathop {\lim }\limits_{x \to – \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = – \infty\)

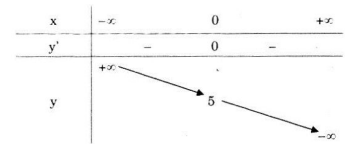
Bảng biến thiên:

 

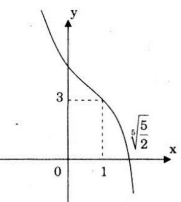
Đồ thị:

Tính đối xứng: \(y”=-12x; y”=0 ⇔ x=0\). Vậy đồ thị hàm số nhận điểm uốn \(I(0;5)\) làm tâm đối xứng.

Đồ thị hàm số cắt trục \(Oy\) tại điểm \((0;5)\), đồ thị cắt trục \(Ox\) tại điểm \(\left( {\sqrt[3]{{\frac{5}{2}}};0} \right).\) 

Bài 2 trang 43 sách sgk giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:

a) \(y=- {x^4} + 8{x^{2}}-1\);               b) \(y= {x^4} – 2{x^2} + 2\);

c) \(y = {1 \over 2}{x^4} + {x^2} – {3 \over 2}\);                 d) \(y =  – 2{x^2} – {x^4} + 3\).

Giải:

 a) Tập xác định: \(\mathbb R\) ;

Sự biến thiên:

\(y’ =-4x^3+ 16x = -4x(x^2- 4)\);

\( y’ = 0  ⇔ x = 0, x = ±2\) .

– Hàm số đồng biến trên khoảng \((-\infty;-2)\) và \((0;2)\); nghịch biến trên khoảng \((-2;0)\) và \(2;+\infty)\).

– Cực trị:

    Hàm số đạt cực đạt tại hai điểm \(x=-2\) và \(x=2\); \(y_{CĐ}=y(\pm 2)=15\).

    Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}=-1\)

– Giới hạn:

\(\mathop {\lim y}\limits_{x \to  \pm \infty }  =  – \infty \)

Bảng biến thiên :

      

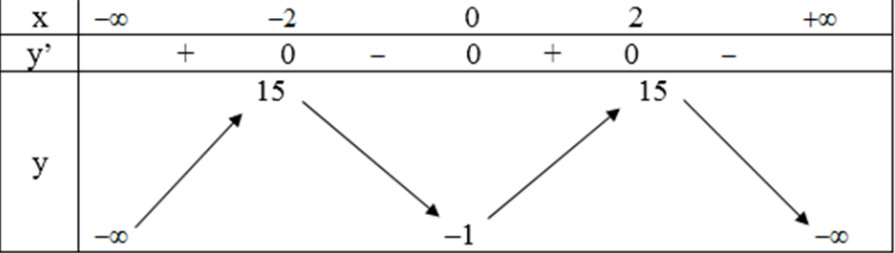
Đồ thị giao \(Oy\) tại điểm \((0;-1)\)

Hàm số đã cho là hàm số chẵn nhận trục \(Oy\) làm trục đối xứng.

 Đồ thị 

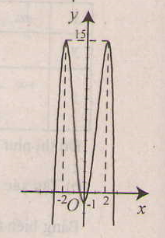
b) Tập xác định: \(\mathbb R\);

Sự biến thiên:

\(y’ =4x^3- 4x = 4x(x^2- 1)\);

\(y’ = 0  ⇔ x = 0, x = ±1\) .

– Hàm số đồng biến trên khoảng \((-1;0)\) và \((1;+\infty)\); nghịch biến trên khoảng \((-\infty;-1)\)  và \((0;1)\).

– Cực trị: 

    Hàm số đạt cực đại tại \(x=0\); \(y_{CĐ}=2\).

    Hàm số đạt cực tiểu tại hai điểm \(x=-1\) và \(x=1\); \(y_{CT}=y(\pm 1)=1\).

-Giới hạn:

\(\mathop {\lim y}\limits_{x \to  \pm \infty }  =  + \infty \)

Bảng biến thiên :

      

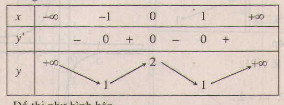
Hàm số đã cho là hàm số chẵn nhận trục \(Oy\) làm trục đối xứng.

Đồ thị giao \(Oy\) tại điểm \((0;2)\)

Đồ thị 

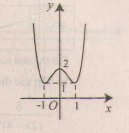
c) Tập xác định: \(\mathbb R\);

Sự biến thiên:

\(y’ =2x^3+ 2x = 2x(x^2+1)\);

\(y’ = 0  ⇔ x = 0\).

– Hàm số nghịch biến trên khoảng \((-\infty;0)\); đồng biến trên khoảng \((0;+\infty)\).

-Cực trị:

    Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}={-3\over 2}\)

-Giới hạn:

\(\mathop {\lim y}\limits_{x \to  \pm \infty }  =  + \infty \)

Bảng biến thiên :

  

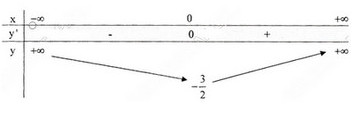
Hàm số đã cho là hàm số chẵn, nhận trục \(Oy\) làm trục đối xứng.

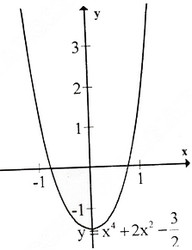
Đồ thị giao \(Ox\) tại hai điểm \((-1;0)\) và \((1;0)\); giao \(Oy\) tại \((0;{-3\over 2})\).

Đồ thị như hình bên.

d) Tập xác định: \(\mathbb R\);

Sự biến thiên:

\(y’ = -4x – 4x^3= -4x(1 + x^2)\);

\(y’ = 0  ⇔ x = 0\).

– Hàm số đồng biến trên khoảng: \((-\infty;0)\); nghịch biến trên khoảng: \((0;+\infty)\).

– Cực trị: Hàm số đạt cực đạt tại \(x=0\); \(y_{CĐ}=3\).

– Giới hạn: 

\(\mathop {\lim y}\limits_{x \to  \pm \infty }  =  -\infty \)

Bảng biến thiên :

         

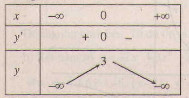
Hàm số đã cho là hàm chẵn, nhận trục \(Oy\) làm trục đối xứng.

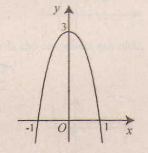
Đồ thị giao \(Ox\) tại hai điểm \((1;0)\) và \((-1;0)\); giao \(Oy\) tại điểm \((0;3)\).

 Đồ thị như hình bên.

Bài 3 trang 43 sách sgk giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số phân thức:

a) \({{x + 3} \over {x – 1}}\) ,

b) \({{1 – 2{\rm{x}}} \over {2{\rm{x}} – 4}}\) ,

c) \({{ – x + 2} \over {2{\rm{x}} + 1}}\)

Giải:

a) Tập xác định : \(\mathbb R{\rm{\backslash \{ }}1\}\);  

* Sự biến thiên:

\(y’ = {{ – 4} \over {{{(x – 1)}^2}}} < 0,\forall x \ne 1\) ;

– Hàm số nghịch biến trên khoảng: \((-\infty;1)\) và \((1;+\infty)\).

– Cực trị:

     Hàm số không có cực trị.

– Tiệm cận:

\(\mathop {\lim y}\limits_{x \to {1^ – }}  =  – \infty \), \(\mathop {\lim y}\limits_{x \to {1^ + }}  =  +\infty\)

\(\mathop {\lim y}\limits_{x \to  \pm \infty }  = 1\)

Do đó, tiệm cận đứng là: \(x = 1\); tiệm cận ngang là: \(y = 1\).

Bảng biến thiên: 

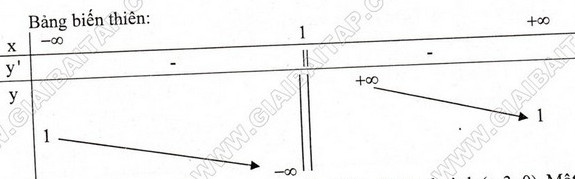
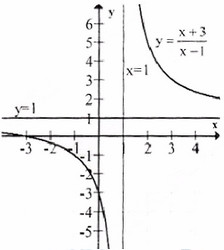
* Đồ thị:

Đồ thị nhận điểm \(I(1;1)\) làm tâm đối xứng.

Đồ thị giao trục tung tại:\((0;-3)\), trục hoành tại \((-3;0)\)

     

             

 

 

 

 

 

 

 

b) Tập xác định : \(\mathbb R \backslash {\rm{\{ }}2\} \);    

* Sự biến thiên:

\(y’ = {6 \over {{{\left( {2{\rm{x}} – 4} \right)}^2}}} > 0,\forall x \ne 2\)

– Hàm số đồng biến trên khoảng: \((-\infty;2)\) và \((2;+\infty)\)

– Cực trị: 

  Hàm số không có cực trị.

– Tiệm cận:

\(\mathop {\lim y}\limits_{x \to {2^ – }}  =  + \infty \), \(\mathop {\lim y}\limits_{x \to {2^ + }}  =  – \infty \), \(\mathop {\lim y}\limits_{x \to  \pm \infty }  =  – 1\)

Do đó, tiệm cận đứng là: \(x = 2\); tiệm cận ngang là:\( y = -1\).

Bảng biến thiên :

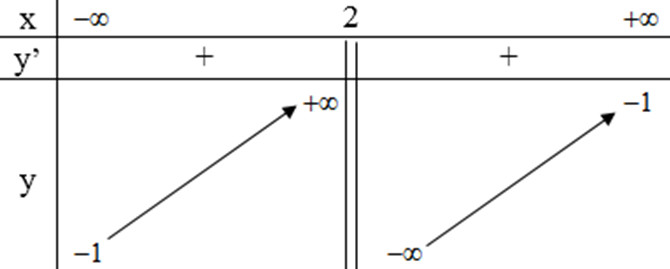
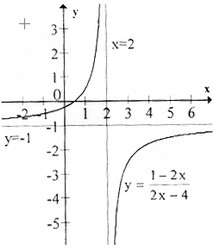
* Đồ thị:

Đồ thị nhận điểm \(I(2;-1)\) lầm tâm đối xứng.

Đồ thị giao trục tung tại: \(\left( {0; – {1 \over 4}} \right)\), trục hoành tại: \(\left( {{1 \over 2};0} \right)\)

c) Tập xác định : \(R\backslash \left\{ { – {1 \over 2}} \right\}\);

Sự biến thiên:

\(y’ = {{ – 5} \over {{{\left( {2{\rm{x}} + 1} \right)}^2}}} < 0,\forall x \ne  – {1 \over 2}\)

– Hàm số nghịch biến trên khoảng: \((-\infty;{-1\over 2})\) và \(({-1\over 2};+\infty)\)

– Cực trị:

Hàm số không có cực trị.

– Tiệm cận:

\(\mathop {\lim y}\limits_{x \to  – {{{1 \over 2}}^ – }}  =  – \infty \), \(\mathop {\lim y}\limits_{x \to  – {{{1 \over 2}}^ + }}  =  + \infty \), \(\mathop {\lim y}\limits_{x \to  \pm \infty }  =  – {1 \over 2}\)

Do đó, tiệm cận đứng là: \(x =  – {1 \over 2}\); tiệm cận ngang là: \(y =  – {1 \over 2}\).

Bảng biến thiên :

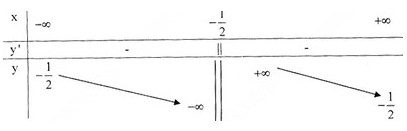
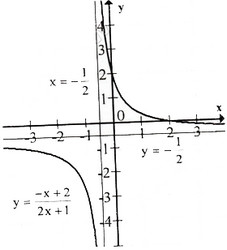
* Đồ thị    

Đồ thị nhận điểm \(I( – {1 \over 2}; – {1 \over 2})\) làm tâm đối xứng.

Đồ thị giao \(Ox\) tại: \((2;0)\), \(Oy\) tại: \((0;2)\)

Giaibaitap.me