Feed Forward Process in Deep Neural Network

Now, we know how with the combination of lines with different weight and biases can result in non-linear models. How does a neural network know what weight and biased values to have in each layer? It is no different from how we did it for the single based perceptron model.

We are still making use of a gradient descent optimization algorithm which acts to minimize the error of our model by iteratively moving in the direction with the steepest descent, the direction which updates the parameters of our model while ensuring the minimal error. It updates the weight of every model in every single layer. We will talk more about optimization algorithms and backpropagation later.

It is important to recognize the subsequent training of our neural network. Recognition is done by dividing our data samples through some decision boundary.

“The process of receiving an input to produce some kind of output to make some kind of prediction is known as Feed Forward.” Feed Forward neural network is the core of many other important neural networks such as convolution neural network.

In the feed-forward neural network, there are not any feedback loops or connections in the network. Here is simply an input layer, a hidden layer, and an output layer.

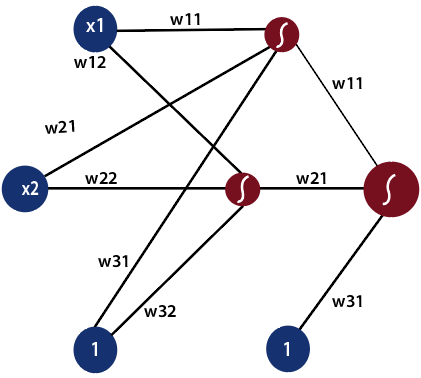
There can be multiple hidden layers which depend on what kind of data you are dealing with. The number of hidden layers is known as the depth of the neural network. The deep neural network can learn from more functions. Input layer first provides the neural network with data and the output layer then make predictions on that data which is based on a series of functions. ReLU Function is the most commonly used activation function in the deep neural network.

To gain a solid understanding of the feed-forward process, let’s see this mathematically.

1) The first input is fed to the network, which is represented as matrix x1, x2, and one where one is the bias value.

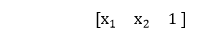
2) Each input is multiplied by weight with respect to the first and second model to obtain their probability of being in the positive region in each model.

So, we will multiply our inputs by a matrix of weight using matrix multiplication.

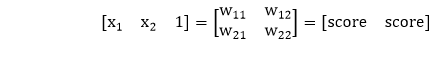
3) After that, we will take the sigmoid of our scores and gives us the probability of the point being in the positive region in both models.

4) We multiply the probability which we have obtained from the previous step with the second set of weights. We always include a bias of one whenever taking a combination of inputs.

And as we know to obtain the probability of the point being in the positive region of this model, we take the sigmoid and thus producing our final output in a feed-forward process.

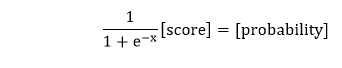
Let takes the neural network which we had previously with the following linear models and the hidden layer which combined to form the non-linear model in the output layer.

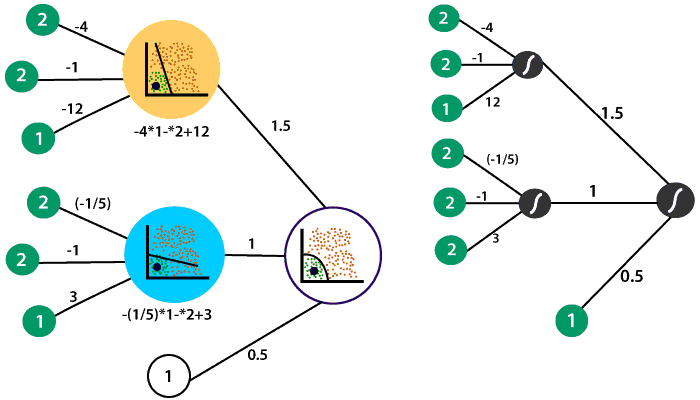
So, what we will do we use our non-linear model to produce an output that describes the probability of the point being in the positive region. The point was represented by 2 and 2. Along with bias, we will represent the input as

The first linear model in the hidden layer recall and the equation defined it

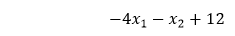
Which means in the first layer to obtain the linear combination the inputs are multiplied by -4, -1 and the bias value is multiplied by twelve.

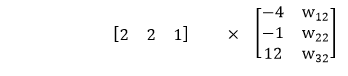
The weight of the inputs are multiplied by -1/5, 1, and the bias is multiplied by three to obtain the linear combination of that same point in our second model.

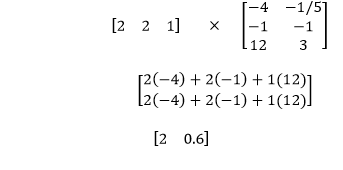
Now, to obtain the probability of the point is in the positive region relative to both models we apply sigmoid to both points as

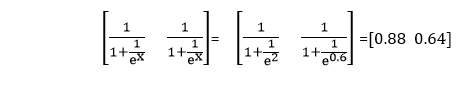
The second layer contains the weights which dictated the combination of the linear models in the first layer to obtain the non-linear model in the second layer. The weights are 1.5, 1, and a bias value of 0.5.

Now, we have to multiply our probabilities from the first layer with the second set of weights as

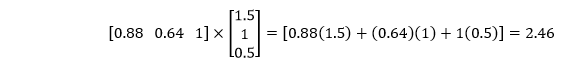
Now, we will take the sigmoid of our final score

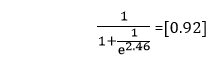
It is complete math behind the feed forward process where the inputs from the input traverse the entire depth of the neural network. In this example, there is only one hidden layer. Whether there is one hidden layer or twenty, the computational processes are the same for all hidden layers.

Next Topic

Backpropagation Process in Deep Neural Network

← prev
next →