Đạo hàm là gì? Khái niệm & Công thức đạo hàm từ A-Z
Với mong muốn lan tỏa kiến thức đến mọi độc giả trên mọi miền tổ quốc. Trong bài viết này manta.edu.vn xin chia sẻ đến bạn đọc công thức đạo hàm đầy đủ nhất từ A đến Z. Bài viết này sẽ giúp các bạn ôn tập kiến thức về đạo hàm một cách đơn giản. Hãy cùng theo dõi thông tin dưới đây nhé!
Đạo hàm là gì? Ý nghĩa của đạo hàm
Trước khi tìm hiểu các công thức đạo hàm, hãy cùng manta.edu.vn tìm hiểu đạo hàm là gì và ý nghĩa của chúng trong quá trình học nhé.
Đạo hàm là gì?
Trong giải tích toán học, đạo hàm là một hàm mô tả sự biến thiên tại một điểm . Nói cách khác, đạo hàm là tỷ số giữa số gia và hàm số tại một điểm x0 . Độ lớn của biến thể và hướng của biến thể đại diện cho giá trị của đạo hàm.
Tuy nhiên, theo một định nghĩa khác của Wikipedia thì đạo hàm được hiểu là sự biến thiên lên xuống của hàm số tại điểm thay đổi. Ngoài ra trong Vật lý đạo hàm được coi là vận tốc tức thời khi một vật đang chuyển động.
Đạo hàm của hàm y=f(x) được ký hiệu là y′(x0) hoặc f′(x0):

- Số gia của đối số là Δx=x−x0
- Số gia của hàm là Δy=y−y0
Ý nghĩa của đạo hàm
Ý nghĩa của đạo hàm được thể hiện qua hai khía cạnh. Một là khía cạnh hình học trong Toán học , hai là khía cạnh Vật lý.
Về mặt hình học cụ thể trong môn Toán lớp 11, đạo hàm có các ý nghĩa sau: Cho hàm số y = f(x) xác định trên khoảng (a;b) và có đạo hàm tại ![]() , gọi (C) là đồ thị của hàm số đó.
, gọi (C) là đồ thị của hàm số đó.

Về mặt vật lý, đạo hàm thứ 11 được coi là vận tốc tức thời khi một vật đang chuyển động. Cụ thể, chúng tôi xem xét chuyển động tuyến tính được xác định bởi phương trình: s = f(t) , trong đó f(t) là một hàm có đạo hàm. Khi đó, vận tốc tức thời xác định tại thời điểm t0 là đạo hàm của hàm s = f(t) tại t0.
![]()
Quy tắc cơ bản khi áp dụng công thức đạo hàm 11

Tổng hợp công thức tính đạo hàm đầy đủ nhất hiện nay
Công thức tính đạo hàm được thể hiện qua một số công thức sau:
1. Công thức đạo hàm cơ bản
Trong quá trình học tập, kiến thức nếu không được rèn luyện và mài dũa sẽ nhanh chóng bị lãng quên. Công thức đạo hàm cũng vậy, dưới đây là bảng đầy đủ các công thức đạo hàm cơ bản bao gồm:
-
Đạo hàm của f(x) trong đó x là biến
-
Đạo hàm của f(u) trong đó u là một hàm số
-
Đạo hàm của một số phân số hữu tỉ

2. Công thức đạo hàm lượng giác
Đạo hàm của hàm lượng giác ngược và hàm lượng giác

3. Công thức C cho đạo hàm cơ bản

4. Công thức C cho đạo hàm cấp cao

Đạo hàm và nguyên hàm trong toán học
Qua những thông tin trên, bạn đọc đã được làm quen với khái niệm đạo hàm. Vì vậy, nguyên thủy trong toán học là gì? Mối quan hệ giữa đạo hàm và nguyên hàm là gì?
Nguyên hàm của một hàm thực f đã cho là một hàm F. Hàm F có đạo hàm bằng f. Sự không xác định là quá trình tìm kiếm nguyên thủy. Tìm biểu thức nguyên hàm khó hơn tìm đạo hàm.
Trong toán học, nguyên hàm được coi là một phần con của đạo hàm. Vì nguyên hàm được định nghĩa từ đạo hàm. Nói cách khác, ngược lại với việc tìm đạo hàm là tìm bản gốc. Qua đó có thể thấy đạo hàm và nguyên hàm trong toán học có mối quan hệ mật thiết với nhau.
Các dạng toán áp dụng đạo hàm, công thức nguyên hàm
Dưới đây là tổng hợp một số dạng toán, bài tập có ví dụ minh họa để các em nắm và hiểu rõ hơn khi áp dụng các công thức đạo hàm:
Dạng 1: Sử dụng khái niệm định nghĩa đạo hàm
Đây là một trong những dạng toán đạo hàm cơ bản, có cách giải đơn giản nhất trong phần bài tập. Để giải bài tập, học sinh sẽ dựa vào định nghĩa và vận dụng các công thức cơ bản để tính toán chính xác. Đặc biệt:

Dạng 2: Chứng minh đẳng thức liên quan đến đạo hàm
Ở dạng bài tập này thường sẽ yêu cầu chứng minh một liên hệ nào đó dựa trên điều kiện cho trước. Yêu cầu học sinh tính toán, chứng minh đẳng thức liên quan đến đạo hàm một cách chính xác và đưa ra kết quả cuối cùng.

Dạng 3: Biết tiếp điểm, viết phương trình tiếp tuyến
Đây là một dạng bài tập áp dụng các công thức đạo hàm khá phổ biến. Cụ thể, bài toán thường sẽ cho phương trình tiếp tuyến của đồ thị hàm số (C): y= f(x), với tiếp điểm M(x0 ; y0) , có dạng: y = y ‘(x0)(x-x0) + y0. Vì vậy, chỉ thay thế các dữ liệu đã cho sẽ tìm thấy câu trả lời chính xác.
Ví dụ: Cho hàm số y= x3 + 3mx2 + ( m+1)x + 1 (1), m là tham số thực. Tìm các giá trị của m để tiếp tuyến của đồ thị hàm số có hoành độ x = -1 và đi qua điểm A(1, 2).
TXD 😀 = RẺ
y’ = f'(x)= 3×2 + 6mx + m + 1
Với x0 = -1 => y0= 2m -1, f'( -1) = -5m + 4
Phương trình tiếp tuyến tại M(-1; 2m – 1) : y= ( -5m + 4 ) ( x+1) + 2m -1 (d)
Ta có A ( 1,2) ∈ (d) <=> ( -5m + 4).2 + 2m – 1 = 2 => m = 5/8
Dạng 4: Viết phương trình tiếp theo khi biết hệ số góc
Viết phương trình tiếp tuyến của (C ) : y = f( x ), biết tiếp tuyến đó có hệ số góc k cho trước
Gọi M(x0 ; y0) là tiếp điểm. Tính y’ => y'(x0)
Phương trình tiếp tuyến Δ có hệ số góc k => y’ = (x0 ) = k(i)
x0 => y0 = f(x0) => : y = k(x – x0 )+ y0
Chú ý: Hệ số góc k = y'(x0 ) của tiếp tuyến Δ thường cho dạng gián tiếp như sau:
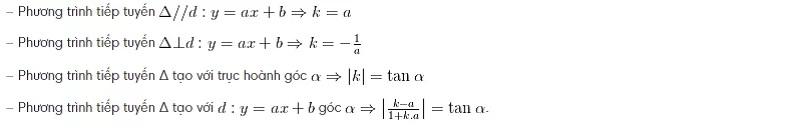
Ví dụ: Cho hàm số y=x3 +3 × 2 – 9x + 5 (C). Tìm tiếp tuyến có hệ số góc nhỏ nhất trong số tất cả các tiếp tuyến của đồ thị (C).
Ta có y’ = f'( x ) = 3×2 + 6x – 9
Gọi x0 là hoành độ của tiếp tuyến nên f'( x0) = 3 x02 + 6 x0 – 9
Ta có 3 x02 + 6×0– 9 =3 ( x02+ 2×0 +1) – 12 = 3 (x0+1)2– 12 > – 12
Vậy min f( x0)= – 12 tại x0= -1 => y0=16
Lập phương trình tiếp tuyến cần tìm: y= -12( x+1)+16 <=> y= -12x + 4
Dạng 5: Bất phương trình và bất phương trình có đạo hàm
Dạng toán này sẽ phải kết hợp nhiều công thức đạo hàm, nguyên hàm để có thể giải các bất phương trình hay hệ phương trình để tìm ra kết quả chính xác.

Dạng 6: Sử dụng công thức đạo hàm nguyên hàm
Với dạng bài tập này, các em phải nắm vững các công thức đạo hàm lớp 11 đã chia sẻ ở trên. Nếu có các hàm phức tạp xuất hiện, bạn có thể rút gọn các hàm rồi tiến hành đạo hàm, đặc biệt là các hàm lượng giác.
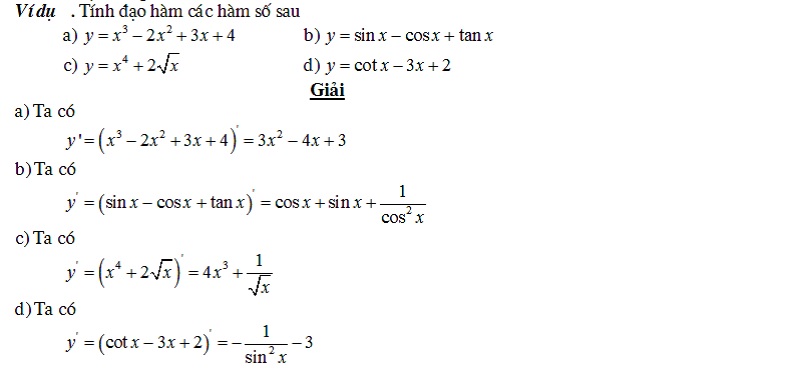
Dạng 7: Tính đạo hàm cấp cao
Đối với các bài tập đạo hàm cấp cao thường thiên về tính đạo hàm cấp 2 trở lên nên có thể áp dụng các công thức tính đạo hàm cấp trên hoặc y(n) = (y(n-1))’ .
Ngoài ra, để tính đạo hàm cấp n, bạn sẽ phải tính đạo hàm từ cấp 1, 2, 3… rồi suy ra công thức tính đạo hàm cấp n.
Một số bài tập tự luyện tính đạo hàm
Dưới đây là một số bài tập để các bạn có thể áp dụng các công thức đạo hàm trên và cùng luyện tập:

Đạo hàm và ứng dụng của đạo hàm
Đạo hàm có nhiều ứng dụng không chỉ trong toán học mà còn trong nhiều lĩnh vực khác. Sau đây là một số ứng dụng của đạo hàm:
Trong Toán học, đạo hàm có ứng dụng là tiếp tuyến của đường con mặt phẳng và phương trình tiếp tuyến.

Trong Vật lý, đạo hàm giúp chúng ta tính toán:
-
Thời gian vận chuyển.
-
Độ lớn tức thời của dòng điện.
-
Gia tốc tức thời
Trong thực tế, đạo hàm được ứng dụng trên đồng hồ xe máy hay khi tính giờ của các vận động viên chạy, bơi tiếp sức… Qua những thông tin trên có thể thấy đạo hàm có rất nhiều ứng dụng trong các lĩnh vực khác nhau. Những khu vực khác nhau.

Phương pháp và cách giải đạo hàm nhanh nhất
Nắm chắc kiến thức về đạo hàm để từ đó vận dụng vào giải các bài tập thực tiễn. Đầu tiên bạn cần nắm vững lý thuyết về đạo hàm từ định nghĩa, tính chất, ý nghĩa, công thức (đạo hàm nhân, chia, công thức đạo hàm giá trị tuyệt đối….). Sau đó cần vận dụng kiến thức đã học để áp dụng vào giải bài tập.
Làm nhiều và đa dạng các dạng bài tập từ cơ bản đến nâng cao sẽ giúp bạn nắm vững kiến thức hơn. Lý thuyết luôn đi đôi với thực hành nên hãy cố gắng vận dụng cả hai yếu tố để học tốt hơn nhé.
Bên cạnh đó, ngày nay nếu chỉ học kiến thức trên lớp là chưa đủ. Bạn có thể tìm thêm kiến thức trên mạng. Một số trang web tính toán đạo hàm trực tuyến miễn phí sẽ giúp bạn kiểm tra đáp án đúng nhanh nhất. Bạn có thể tính đạo hàm mathway ngay tại trang web của mathway, hoặc trong mục ” kiến thức cơ bản ” của manta.edu.vn cũng có nhiều mục về đạo hàm để bạn tham khảo.
Trên đây là những kiến thức bổ ích về các công thức đạo hàm thông dụng nhất. Hi vọng qua bài viết các bạn đã nắm được công thức đạo hàm và ứng dụng của nó trong thực tế. Từ đó vận dụng chúng để giải quyết các vấn đề và đạt kết quả học tập tốt.















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


