Bài 11: Số vô tỉ. Khái niệm về căn bậc hai
1. Số vô tỉ
Ta xét bài toán sau:
Cho hình vuông \(AEBF\) có cạnh bằng \(1\left(m\right)\) (hình vẽ). Hình vuông \(ABCD\) có cạnh \(AB\) là đường chéo của \(AEBF\).
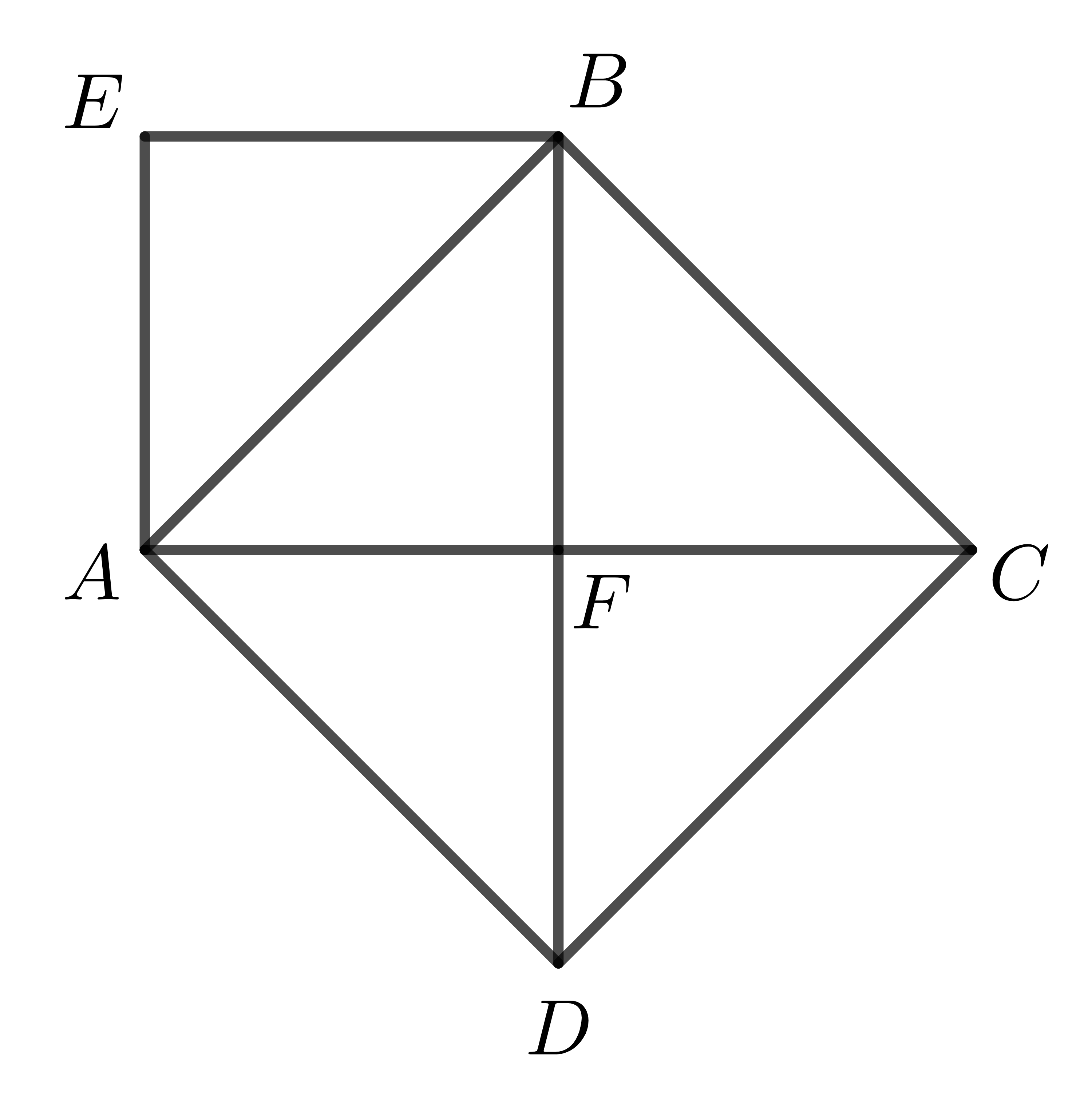
a) Tính diện tích hình vuông \(ABCD\).
b) Tính độ dài cạnh \(AB\).
Lời giải
a) Diện tích hình vuông \(AEBF\) là: \(S_{AEBF}=1.1=1\left(m^2\right).\)
Ta dễ dàng nhận thấy diện tích hình vuông \(ABCD\) gấp hai lần diện tích hình vuông \(AEBF\).
Do đó, diện tích hình vuông \(ABCD\) là: \(S_{ABCD}=2.1=2\left(m^2\right).\)
b) Giả sử \(AB=x\left(m\right)\left(x>0\right)\).
Do \(S_{ABCD}=2\left(m^2\right)\) nên ta suy ra \(x^2=2\).
Nhiệm vụ của ta là đi tìm số \(x\) thỏa mãn \(x^2=2\), số \(x\) đó chính là độ dài cạnh \(AB\).
Người ta đã chứng minh được rằng, không có số hữu tỉ nào có bình phương bằng \(2\).
Thay vào đó, người ta tính được:
\(x=1,4142135623730950488016887…\)
Nhận thấy, số trên là một số thập phân vô hạn mà phần thập phân của nó không có một chu kì nào cả.
Ta gọi đó là số thập phân vô hạn không tuần hoàn.
Các số như vậy được gọi là các số vô tỉ.
Như vậy:
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Kí hiệu: Ta kí hiệu tập hợp số vô tỉ bởi chữ \(I\).
@54051@
2. Khái niệm căn bậc hai
Trong ví dụ ở phần trên, ta thấy số \(x\) cần tìm là một số thỏa mãn \(x^2=2\). Ta nói “\(x\) là một căn bậc hai của \(2\)”.
Ta lại có: \(2^2=4;\left(-2\right)^2=4\). Ta nói “\(2\) và \(-2\) là các căn bậc hai của \(4\)”.
Tương tự, \(5^2=25;\left(-5\right)^2=25\) nên “\(5\) và \(-5\) là các căn bậc hai của \(25\)”.
Định nghĩa: Căn bậc hai của một số \(a\) không âm là số \(x\) sao cho \(x^2=a\).
Ví dụ:
+) Căn bậc hai của \(16\) là \(4\) và \(-4\) (do \(4^2=16;\left(-4\right)^2=16\)).
+) Căn bậc hai của \(144\) là \(12\) và \(-12\) (do \(12^2=144;\left(-12\right)^2=144\)).
+) Căn bậc hai của \(0\) là \(0\) (do \(0^2=0\)).
Người ta đã chứng minh được kết quả sau:
Tính chất:
- Số dương
\(a\)
có hai căn bậc hai: một số dương (kí hiệu là
\(\sqrt{a}\)
) và một số âm (kí hiệu là
\(-\sqrt{a}\)
).
- Số
\(0\)
chỉ có đúng một căn bậc hai là chính nó, viết là
\(\sqrt{0}=0\)
.
- Số âm không có căn bậc hai.
Nhận xét:
- Hai căn bậc hai của số một số dương là hai số đối nhau.
- Ta cần ghi nhớ sự tương ứng về kí hiệu và căn bậc hai của một số. Khi viết
\(\sqrt{a}\)
, ta hiểu đó là giá trị không âm.
Chú ý: Không được viết \(\sqrt{4}=\pm2\) !
Ví dụ:
+) Số \(81\) có hai căn bậc hai là \(\sqrt{81}=9;-\sqrt{81}=-9.\)
+) Số \(400\) có hai căn bậc hai là \(\sqrt{400}=20;-\sqrt{400}=-20.\)
+) Số \(2\) có hai căn bậc hai là \(\sqrt{2}\) và \(-\sqrt{2}\).
@54050@
Như vậy, trong bài toán ở phần trên, ta có \(x^2=2\) và \(x>0\) nên \(x=\sqrt{2}\left(m\right)\). \(\sqrt{2}\) chính là độ dài đường chéo của hình vuông có cạnh bằng \(1\).
Lưu ý: Người ta chứng minh được rằng: \(\sqrt{2},\sqrt{3},\sqrt{5},\sqrt{6},\sqrt{7},…\) là các số vô tỉ.
Ví dụ 2: Tìm \(x\) biết
a) \(\sqrt{3x}=6\);
b) \(x^2=15\);
c) \(\left(3x-2\right)^2=121\).
Lời giải
a) Ta có \(6^2=36\Rightarrow6=\sqrt{36}\)
\(\Rightarrow3x=36\Rightarrow x=12\).
Vậy \(x=12\) là giá trị cần tìm.
b) Ta có \(x^2=15\) suy ra \(x=\sqrt{15}\) hoặc \(x=-\sqrt{15}\).
c) Ta có \(\left(3x-2\right)^2=121\)
Trường hợp 1: \(3x-1=\sqrt{121}\)
\(\Rightarrow3x-1=11\Rightarrow3x=12\Rightarrow x=4\).
Trường hợp 2: \(3x-1=-\sqrt{121}\)
\(\Rightarrow3x-1=-11\Rightarrow3x=-10\Rightarrow x=\dfrac{-10}{3}\).
Vậy \(x=4\) hoặc \(x=\dfrac{-10}{3}\) là giá trị cần tìm.
@958315@















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


