Bài 1 : KHÁI NIỆM HÀM SỐ

Posted 20/06/2011 by Trần Thanh Phong in Lớp 9, Đại số 9. Tagged: hàm số. 23 bình luận

Bài 1 :

KHÁI NIỆM HÀM SỐ

–o0o–

Nếu một đại lượng y phụ thuộc vào một đại lượng thay đổi x sao cho một giá trị của xha ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x, và x gọi là biến số.

1. Hàm số được cho bằng hai dạng : bảng và công thức.

a. Hàm số dạng bảng :

x
0
1
2
3
4
5

y
1
3
5
7
9
11

Mục Lục

b. Hàm số bằng công thức (dạng tường minh):

y = f(x)

f(x) là biểu thức đại số với biến x.

Ví dụ :

y = 2 : hàm hằng.

y = 2x +1: hàm số bậc nhất

y = x2 +2x -1: hàm số bậc 2

$y=\frac{2x+1}{x-1}$ hàm số nhất biến .v .v …

2. Tập giá trị và tập xác định :

Tập giá trị Y là tập hợp các giá trị của hàm số y.

Tập xác định X tập hợp các giá trị của biến số x. Tập xác định X của hàm số y xác định.

3. Đồ thị của hàm số :

3.a. Định nghĩa :

Đồ thị của hàm số y = f(x) là tập hợp các cặp giá trị tương ứng (x ; f(x)) trên mặt phẳng tọa độ.

b. mặt phẳng tọa độ Oxy :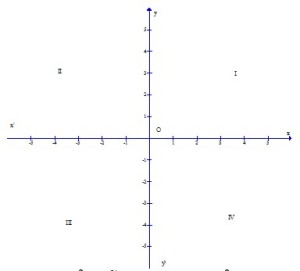

* Ox :trục hoành.

* Oy : trục tung.

* O : gốc tọa độ.

* ( I) góc phần tư thứ I, (II) góc phần tư thứ iI,( III) góc phần tư thứ III,( IV) góc phần tư thứ IV.

c. Biểu diễn tọa độ một điểm A trên mặt phẳng tọa độ Oxy:

Ta có : A(xA ; yA) trong đó : xA: hoành độ của điểm A .

yA: hoành độ của điểm A .

ví dụ Biểu diễn tọa độ một điểm A(2 ; 3)

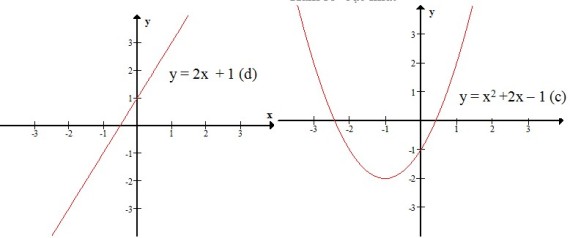
vẽ đồ thị của một hàm số trên mặt phẳng tọa độ:

y = x2 +2x – 1 (c); y = 2x + 1 (d)

4. Vị trí tương đối giữa điểm và đồ thị hàm số :

cho A(xA ; yA) và hàm số y = f(x) có đồ thị (c). A thuộc (c) khi yA = f(xA)

ví dụ : A(1 ; 2) và B( -2 ; 1) có thuộc y = f(x) = x2 +2x – 1 (c)

giải.

Tính : f(xA) = f(1) = 12 +2.1 – 1 = 2 = yA

=> A € ( c).

f(xB) = f(-2) = (-2)2 +2.(-2) – 1 = 2 = -1 ≠ yB

=> B không nằm trên (C).

5. Hàm số đồng biến và hàm số nghịch biến :

Định nghĩa :

Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc R.

Nếu giá trị của biến tăng lên mà giá trị tương ứng của hàm số f(x) cũng tăng lên
thì hàm số y = f(x) được gọi là hàm số đồng biến trên R (gọi tắt là hàm số đồng biến).
Nếu giá trị của biến tăng lên mà giá trị tương ứng của hàm số f(x) cũng giảm đi
thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến).

Định lí : với x1, x2 thuộc R.