30 bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số mức độ nhận biết
Câu hỏi 1 :
Hàm số 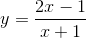 đồng biến trên
đồng biến trên
-
A
R
-
B
R\{-1}
-
C
\(\left( { – \infty ;-1} \right)\) và \(\left( {-1; + \infty } \right)\)
-
D
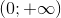
Đáp án: C
Lời giải chi tiết:
TXĐ: D=R\{-1}
\(y’ = {3 \over {{{\left( {x + 1} \right)}^2}}} > 0\,\,\forall x \in D \).
Do đó hàm số đồng biến trên \(\left( { – \infty ;-1} \right)\) và \(\left( {-1; + \infty } \right)\)
Đáp án – Lời giải
Câu hỏi 2 :
Hàm số \(y = 2{x^4} + 1\) đồng biến trên khoảng nào?
-
A
\(\left( {0; + \infty } \right)\)
-
B
\(\left( { – \dfrac{1}{2}; + \infty } \right)\)
-
C
\(\left( { – \infty ; – \dfrac{1}{2}} \right)\)
-
D
\(\left( { – \infty ;0} \right)\)
Đáp án: A
Lời giải chi tiết:
Phương pháp: Tìm khoảng đồng biến (nghịch biến) của 1 hàm số:
+ Tính \(y’\), giải phương trình \(y’ = 0\)
+ Giải các bất phương trình \(y’ > 0\) và \(y’ < 0\)
+ Khoảng đồng biến của hàm số là khoảng \((a;b)\) mà \(y’ \geqslant 0,\forall x \in \left( {a;b} \right)\) và có hữu hạn giá trị \(x\) để \(y’ = 0\) . Tương tự với khoảng nghịch biến của hàm số.
Cách giải
Ta có \(y’ = 8{x^3} = 0 \Leftrightarrow x = 0;y’ > 0 \Leftrightarrow x > 0\)
Vậy hàm số đã cho đồng biến trên \(\left( {0; + \infty } \right)\)
Chọn đáp án A
Đáp án – Lời giải
Câu hỏi 3 :
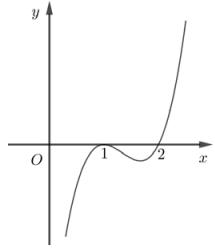
Hình bên là đồ thị hàm số \(y = f’\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
-
A
\(\left( {0;1} \right)\) và \(\left( {2; + \infty } \right)\)
-
B
\(\left( {1;2} \right)\)
-
C
\(\left( {2; + \infty } \right)\)
-
D
\(\left( {0;1} \right)\)
Đáp án: C
Phương pháp giải:
Khi đạo hàm của hàm số mang dấu dương trên một khoảng thì hàm số đồng biến trên khoảng đó và ngược lại
Lời giải chi tiết:
Hàm số \(y = f’\left( x \right)\) dương trong khoảng \(\left( {2; + \infty } \right)\)
\( \Rightarrow \) Hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
Chọn đáp án C
Đáp án – Lời giải
Câu hỏi 4 :
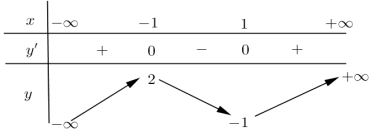
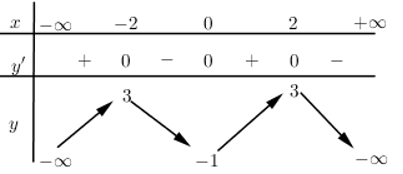
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left( {-\infty ; + \infty } \right)\), có bảng biến thiên như hình sau:
Mệnh đề nào sau đây đúng?
-
A
Hàm số nghịch biến trên khoảng \(\left( {1; + \infty } \right)\)
-
B
Hàm số đồng biến trên khoảng \(\left( {-\infty ;-2} \right)\)
-
C
Hàm số nghịch biến trên khoảng \(\left( {-\infty ;1} \right)\)
-
D
Hàm số đồng biến trên khoảng \(\left( {-1; + \infty } \right)\)
Đáp án: B
Phương pháp giải:
Phương pháp:
Tại các khoảng \(y’ > 0\) thì hàm số đồng biến, tại các khoảng \(y’ < 0\) thì hàm số nghịch biến.
Lời giải chi tiết:
Dựa vào bảng biến thiên ta thấy
Hàm số đồng biến trên \(\left( {1; + \infty } \right)\)
Hàm số đồng biến trên \(\left( {-\infty ;-1} \right)\) do đó cũng đồng biến trên \(\left( {-\infty ;-2} \right)\)
Trên các khoảng \(\left( {-\infty ;1} \right)\) và \(\left( {-1; + \infty } \right)\) hàm số không đơn điệu (đồng biến hay nghịch biến)
Chọn đáp án B
Đáp án – Lời giải
Câu hỏi 5 :
Tìm tập hợp các giá trị của m để hàm số \(y=\frac{x-m}{x+1}\) nghịch biến trên từng khoảng xác định là:
-
A
\(\left( -\infty ;-1 \right)\).
-
B
\(\left( -\infty ;1 \right]\).
-
C
\(\left( -\infty ;-1 \right]\).
-
D
\(\left( -1;+\infty \right)\).
Đáp án: A
Phương pháp giải:
Tìm m để y’ < 0
Lời giải chi tiết:
Hàm số đã cho nghịch biến trên từng khoảng \(\Leftrightarrow y’=\frac{1+m}{{{\left( x+1 \right)}^{2}}}<0\Leftrightarrow m<-1\)
Chọn đáp án A
Đáp án – Lời giải
Câu hỏi 6 :
Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số \(y = {x^3} – 3{x^2} + 1\)?
-
A
Hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
-
B
Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\)
-
C
Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\)
-
D
Hàm số đồng biến trên khoảng \(\left( { – \infty ;2} \right)\)
Đáp án: B
Phương pháp giải:
– Tính \(y’\), tìm các nghiệm của \(y’ = 0\).
– Tìm các khoảng dương, âm của \(y’\) và kết luận.
Lời giải chi tiết:
Ta có:
\(y’ = 3{x^2} – 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
\(y’ > 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < 0\end{array} \right.\) nên hàm số đồng biến trên các khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
\(y’ < 0 \Leftrightarrow 0 < x < 2\) nên hàm số nghịch biến trên \(\left( {0;2} \right)\).
Chọn B.
Đáp án – Lời giải
Câu hỏi 7 :
Cho hàm số \(y = \dfrac{{x + 3}}{{x + 2}}.\) Khẳng định nào sau đây đúng?
-
A
Hàm số nghịch biến trên mỗi khoảng \(\left( { – \infty ; – 3} \right)\,\, \cup \,\,\left( { – 2; + \infty } \right).\)
-
B
Hàm số nghịch biến trên mỗi khoảng \(\left( { – \infty ; – 3} \right)\) và \(\left( { – 2; + \infty } \right).\)
-
C
Hàm số nghịch biến trên R.
-
D
Hàm số ngịch biến trên \(R\backslash \left\{ 2 \right\}.\)
Đáp án: B
Phương pháp giải:
+) Xác định TXĐ của hàm số.
+) Tính y’ và xét tính đơn điệu của hàm số trên TXĐ của hàm số.
Lời giải chi tiết:
TXĐ: \(D = R\backslash \left\{ { – 2} \right\}.\)
Có \(y’ = \dfrac{{1.2 – 3.1}}{{{{\left( {x + 2} \right)}^2}}} = – \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} < 0\,\,\,\forall x \in D\)
\( \Rightarrow \)Hàm số nghịch biến trên mỗi khoảng \(\left( { – \infty ; – 3} \right)\) và \(\left( { – 2; + \infty } \right).\)
Chọn B.
Đáp án – Lời giải
Câu hỏi 8 :
Hàm số \(y=\frac{{{x}^{4}}}{4}-2{{x}^{2}}+3\) nghịch biến trên khoảng nào?
-
A
\(\left( -\infty ;-2 \right)\) và \(\left( 0;2 \right)\)
-
B
\(\left( -2;0 \right)\)
-
C
\(\left( 2;+\infty \right)\)
-
D
\(\left( -2;0 \right)\) và \(\left( 2;+\infty \right)\)
Đáp án: A
Phương pháp giải:
– Tính \(y’\) và tìm các khoảng làm cho \(y'<0\).
Lời giải chi tiết:
Ta có: \(y’={{x}^{3}}-4x\)
\(y’ = 0 \Rightarrow {x^3} – 4x = 0 \Leftrightarrow x\left( {x – 2} \right)\left( {x + 2} \right) = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x = – 2\\x = 2\end{array} \right.\)
Xét dấu :
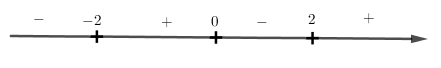
Từ bảng xét dấu ta dễ dàng quan sát được hàm số nghịch biến trên các khoảng \(\left( -\infty ,-2 \right)\) và \(\left( 0,2 \right)\).
\(\Rightarrow \)
Đáp án A
Đáp án – Lời giải
Câu hỏi 9 :
Cho hàm số : \(y = {x^3} – 3{{\rm{x}}^2} – 3\). Mệnh đề nào dưới đây đúng
-
A
Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\)
-
B
Hàm số nghịch biến trên khoảng \(\left( { – \infty ;0} \right)\)
-
C
Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
-
D
Hàm số nghịch biến trên khoảng \(\left( {2; + \infty } \right)\)
Đáp án: C
Phương pháp giải:
– Tính \(y’\), tìm các nghiệm của \(y’\).
– Hàm số đồng biến trên \(\left( {a;b} \right)\) nếu \(y’ > 0,\forall x \in \left( {a;b} \right)\).
Lời giải chi tiết:
Ta có:
\(y’ = 3{{\rm{x}}^2} – 6{\rm{x}} = 3{\rm{x}}\left( {x – 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Bảng biến thiên
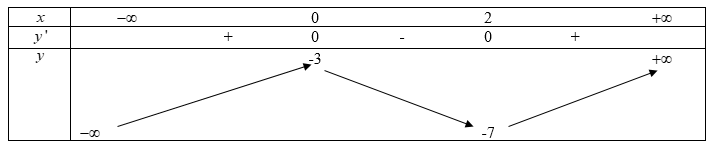
Từ bảng biến thiên ta có hàm số đồng biến trên khoảng\(\left( {2; + \infty } \right)\)
Đáp án C
Đáp án – Lời giải
Câu hỏi 10 :
Cho hàm số \(y = \frac{{x – 2}}{{x – 1}}.\) Khẳng định nào sau đây là khẳng định đúng?
-
A
Hàm số nghịch biến trên \(R\backslash \left\{ 1 \right\}.\)
-
B
Hàm số đồng biến trên \(R\backslash \left\{ 1 \right\}.\)
-
C
Hàm số đơn điệu trên R.
-
D
Hàm số đồng biến trên các khoảng \(\left( { – \infty ;\,\,1} \right)\) và \(\left( {1; + \infty } \right).\)
Đáp án: D
Phương pháp giải:
Hàm số dạng \(y = \frac{{ax + b}}{{cx + d}}\) luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.
Lời giải chi tiết:
Cách giải:
Tập xác định: \(D = R\backslash \left\{ 1 \right\}.\)
Ta có: \(y’ = \frac{{ – 1 + 2}}{{{{\left( {x – 1} \right)}^2}}} = \frac{1}{{{{\left( {x – 1} \right)}^2}}} > 0\,\,\,\forall x \in D.\)
Vậy hàm số đồng biến trên các khoảng \(\left( { – \infty ;\,\,1} \right)\) và \(\left( {1; + \infty } \right).\)
Đáp án – Lời giải
Câu hỏi 11 :
Trong các hàm số sau, hàm số nào đồng biến trên R?
-
A
\(y = {x^3} + 3x + 2\)
-
B
\(y = {x^3} – 3x + 2\)
-
C
\(y = {x^4} + 3{x^2} + 2\)
-
D
\(y = \dfrac{{x – 1}}{{x + 1}}\)
Đáp án: A
Phương pháp giải:
Hàm số \(y = f\left( x \right)\) đồng biến trên \(R \Leftrightarrow f’\left( x \right) \ge 0\forall x \in R\) và chỉ bằng 0 tại hữu hạn điểm.
Lời giải chi tiết:
Nhận thấy \(y = {x^3} + 3x + 2 \Rightarrow y’ = 3{x^2} + 3 > 0\,\,\,\forall x \in R\) nên hàm số \(y = {x^3} + 3x + 2\) đồng biến trên R.
Chọn A.
Đáp án – Lời giải
Câu hỏi 12 :
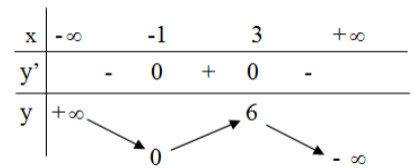
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ dưới đây. Khẳng định nào sau đây là sai?
-
A
\(f\left( x \right)\) nghịch biến trên khoảng \(\left( -\infty ;-1 \right)\).
-
B
\(f\left( x \right)\) đồng biến trên khoảng \(\left( 0;6 \right)\).
-
C
\(f\left( x \right)\) nghịch biến trên khoảng \(\left( 3;+\infty \right)\).
-
D
\(f\left( x \right)\) đồng biến trên khoảng \(\left( -1;3 \right)\).
Đáp án: B
Phương pháp giải:
Sử dụng kĩ năng đọc BBT và tính đồng biến và nghịch biến của hàm số.
Lời giải chi tiết:
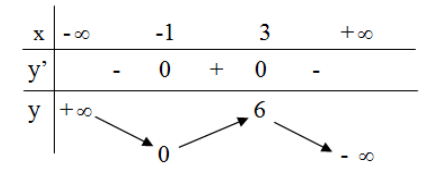
Trên khoảng từ \(\left( 0;6 \right)\) ta thấy hàm số đồng biến trên khoảng \(\left( 0;3 \right)\) và nghịch biến trên khoảng \(\left( 3;6 \right)\) nên đáp án B sai.
Chọn B.
Đáp án – Lời giải
Câu hỏi 13 :
Hàm số \(y={{x}^{3}}-3x+12\) đồng biến trên khoảng nào trong các khoảng sau đây?
-
A
\(\left( 0;+\infty \right)\)
-
B
\(\left( -\infty ;-1 \right)\)
-
C
\(\left( -\infty ;1 \right)\)
-
D
\(\left( -1;1 \right)\)
Đáp án: B
Phương pháp giải:
– Bước 1: Tìm TXĐ của hàm số.
– Bước 2: Tính đạo hàm \(f’\left( x \right)\), tìm các điểm \({{x}_{1}},{{x}_{2}},…,{{x}_{n}}\) mà tại đó đạo hàm bằng \(0\) hoặc không xác định.
– Bước 3: Xét dấu đạo hàm và nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
+ Các khoảng mà \(f’\left( x \right)>0\) là các khoảng đồng biến của hàm số.
+ Các khoảng mà \(f’\left( x \right)<0\) là các khoảng nghịch biến của hàm số.
Lời giải chi tiết:
TXĐ: \(D=R\)
Ta có: \(y={{x}^{3}}-3x+12\Rightarrow y’=3{{x}^{2}}-3=0\Leftrightarrow x=\pm 1\)
\(y’>0\Leftrightarrow 3{{x}^{2}}-3>0\Leftrightarrow \left[ \begin{align} & x>1 \\ & x<-1 \\ \end{align} \right.\) nên hàm số đồng biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( 1;+\infty \right)\)
Chọn B.
Đáp án – Lời giải
Câu hỏi 14 :
Cho hàm số \(y=\frac{2x+1}{1-x}\). Mệnh đề nào sau đây đúng ?
-
A
Hàm số nghịch biến trên \(\left( -\infty ;1 \right)v\text{ }\!\!\grave{\mathrm{a}}\!\!\text{ }\left( 1;+\infty \right)\).
-
B
Hàm số đồng biến trên\(R\backslash \left\{ 1 \right\}\).
-
C
Hàm số đồng biến trên \(\left( -\infty ;1 \right)v\text{ }\!\!\grave{\mathrm{a}}\!\!\text{ }\left( 1;+\infty \right)\).
-
D
Hàm số đồng biến trên \(\left( -\infty ;1 \right)\cup \left( 1;+\infty \right)\).
Đáp án: C
Phương pháp giải:
Sử dụng cách xét tính đơn điệu của hàm số.
Lời giải chi tiết:
Txđ : \(D=\mathbb{R}\backslash \left\{ 1 \right\}\)
Có : \(y’=\frac{3}{{{\left( 1-x \right)}^{2}}}>0,\forall x\ne 1\)
\(\Rightarrow \) Hàm số đồng biến trên \(\left( -\infty ;1 \right)v\text{ }\!\!\grave{\mathrm{a}}\!\!\text{ }\left( 1;+\infty \right)\).
Chọn C.
Đáp án – Lời giải
Câu hỏi 15 :
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
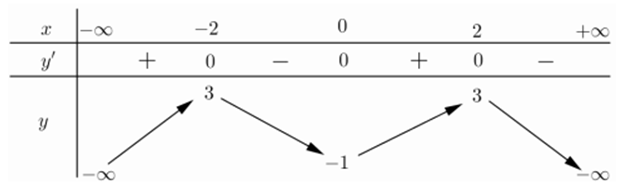
Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
-
A
\(\left( -2;0 \right)\)
-
B
\(\left( -\infty ;-2 \right)\)
-
C
\(\left( 0;2 \right)\)
-
D
\(\left( 0;+\infty \right)\)
Đáp án: A
Phương pháp giải:
Hàm số \(y=f\left( x \right)\) nghịch biến trên các khoảng làm cho đạo hàm mang dấu âm.
Lời giải chi tiết:
Quan sát bảng biến thiên ta thấy hàm số nghịch biến trên các khoảng \(\left( -2;0 \right)\) và \(\left( 2;+\infty \right)\).
Chọn A.
Đáp án – Lời giải
Câu hỏi 16 :
Hàm số \(y={{x}^{3}}-3x\) nghịch biến trên khoảng nào?
-
A
\(\left( -\infty ;-1 \right)\).
-
B
\(\left( -\infty ;+\infty \right)\).
-
C
\(\left( -1;1 \right)\).
-
D
\(\left( 0;+\infty \right)\).
Đáp án: C
Phương pháp giải:
– Tính \(y’\) và tìm các nghiệm của \(y’=0\) và các điểm làm cho đạo hàm không xác định.
– Xét dấu \(y’\) và tìm các khoảng làm cho \(y'<0\) là các khoảng nghịch biến của hàm số.
Lời giải chi tiết:
\(\begin{array}{l}y = {x^3} – 3x \Rightarrow y = 3{x^2} – 3\\y’ = 0 \Leftrightarrow x = \pm 1\end{array}\)
Bảng xét dấu y’:
![]()
Vậy hàm số \(y={{x}^{3}}-3x\) nghịch biến trên khoảng\(\left( -1;1 \right)\).
Chọn: C.
Đáp án – Lời giải
Câu hỏi 17 :
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên sau. Tìm mệnh đề đúng?
-
A
Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng \(\left( -2;\ 0 \right).\)
-
B
Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng \(\left( -4;\ 0 \right).\)
-
C
Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \(\left( -\infty ;\ 0 \right).\)
-
D
Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \(\left( -4;\ +\infty \right).\)
Đáp án: A
Phương pháp giải:
+) Dựa vào những kiến thức cơ bản của hàm số và quan sát bảng biến thiên để đưa ra kết luận đúng.
Lời giải chi tiết:
Dựa vào BBT ta thấy đáp án A đúng.
Chọn A
Đáp án – Lời giải
Câu hỏi 18 :
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
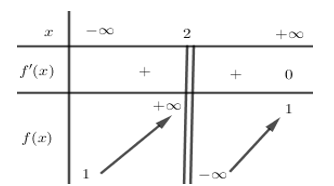
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A
\(\left( 1;+\infty \right)\).
-
B
\(\left( 0;3 \right)\).
-
C
\(\left( -\infty ;+\infty \right)\).
-
D
\(\left( 2;+\infty \right)\).
Đáp án: D
Phương pháp giải:
Sử dụng các đọc BBT: nếu \({f}’\left( x \right)>0,\forall x\in \left( a;b \right)\) thì \(f\left( x \right)\) đồng biến trên \(\left( a;b \right)\).
Lời giải chi tiết:
Từ BBT ta thấy \({f}’\left( x \right)>0,\forall x\in \left( 2;+\infty \right)\)nên hàm số đồng biến trên khoảng \(\left( 2;+\infty \right)\).
Chọn D.
Đáp án – Lời giải
Câu hỏi 19 :
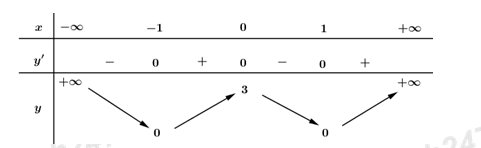 Cho hàm số có bảng biến thiên như sau:
Cho hàm số có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
-
A
Hàm số đồng biến trên các khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right)\).
-
B
Hàm số nghịch biến trên các khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right)\).
-
C
Hàm số đồng biến trên các khoảng \(\left( 0;\ 3 \right)\) và \(\left( 0;+\infty \right).\)
-
D
Hàm số đồng biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( 0;1 \right).\)
Đáp án: A
Phương pháp giải:
Dựa vào bảng biến thiên để nhận xét tính đơn điệu của hàm số.
Lời giải chi tiết:
Dựa vào bàng biến thiên ta thấy hàm số đồng biến trên các khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right).\)
Hàm số nghịch biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( 0;\ 1 \right).\)
Chọn A.
Đáp án – Lời giải
Câu hỏi 20 :
Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên khoảng \(\left( a;b \right).\) Mệnh đề nào sau đây sai ?
-
A
Nếu \({f}’\left( x \right)<0\) với mọi \(x\in \left( a;b \right)\) thì hàm số \(y=f\left( x \right)\) nghịch biến trên \(\left( a;b \right).\)
-
B
Nếu \({f}’\left( x \right)>0\) với mọi \(x\in \left( a;b \right)\) thì hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( a;b \right).\)
-
C
Nếu hàm số \(y=f\left( x \right)\) nghịch biến trên \(\left( a;b \right)\) thì \({f}’\left( x \right)\le 0\) với mọi \(x\in \left( a;b \right).\)
-
D
Nếu hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( a;b \right)\) thì \({f}’\left( x \right)>0\) với mọi \(x\in \left( a;b \right).\)
Đáp án: D
Phương pháp giải:
Lý thuyết về tính đơn điệu (đồng biến – nghịch biến) của hàm số
Lời giải chi tiết:
Nếu hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( a;b \right)\) thì \({f}’\left( x \right)\ge 0\) với mọi \(x\in \left( a;b \right).\)
Chọn D
Đáp án – Lời giải
Câu hỏi 21 :
Cho đồ thị hàm số như hình vẽ
Mệnh đề nào dưới đây là đúng ?
-
A
Hàm số nghịch biến trên \(\left( -\,\infty ;-\,1 \right).\)
-
B
Hàm số luôn đồng biến trên \(\mathbb{R}.\)
-
C
Hàm số đồng biến trên \(\left( -\,1;+\,\infty \right).\)
-
D
Hàm số nghịch biến trên \(\left( 1;+\,\infty \right).\)
Đáp án: A
Phương pháp giải:
Đọc đồ thị hàm số để xác định khoảng đồng biến – nghịch biến.
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy hàm số nghịch biến trên khoảng \(\left( -\,\infty ;-\,1 \right)\) và \(\left( 0;\ 1 \right).\)
Chọn A
Đáp án – Lời giải
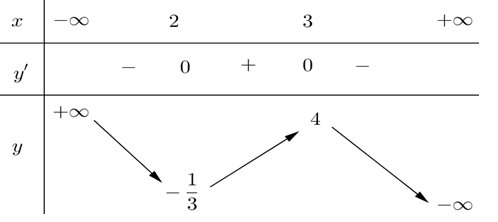
Câu hỏi 22 :
Cho hàm số phù hợp với bảng biến thiên sau
Phát biểu nào sau đây là đúng ?
-
A
Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;-\,\frac{1}{3} \right);\,\,\left( 1;+\,\infty \right)\) và đồng biến trên khoảng \(\left( -\frac{1}{3};1 \right).\)
-
B
Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;2 \right)\cup \left( 3;+\,\infty \right)\) và đồng biến trên khoảng \(\left( 2;3 \right).\)
-
C
Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;-\,\frac{1}{3} \right)\cup \left( 1;+\,\infty \right)\) và đồng biến trên khoảng \(\left( -\frac{1}{3};1 \right).\)
-
D
Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;2 \right);\,\,\left( 3;+\,\infty \right)\) và đồng biến trên khoảng \(\left( 2;3 \right).\)
Đáp án: D
Phương pháp giải:
Dựa vào bảng biến thiên và mũi tên để xác định khoảng đồng biến và nghịch biến của hàm số
Lời giải chi tiết:
Dựa vào bảng biến thiên, ta thấy rằng hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;2 \right);\,\,\left( 3;+\,\infty \right)\) và đồng biến trên khoảng \(\left( 2;3 \right).\)
Chọn D.
Đáp án – Lời giải
Câu hỏi 23 :
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y=\frac{x+{{m}^{2}}}{x+1}\) luôn đồng biến trên từng khoảng xác định.
-
A
\(m\in \left[ -\,1;1 \right].\)
-
B
\(m\in \mathbb{R}.\)
-
C
\(m\in (-1;1).\)
-
D
\(m\in \left( -\,\infty ;-\,1 \right)\cup \left( 1;+\,\infty \right).\)
Đáp án: C
Phương pháp giải:
Hàm số bậc nhất trên bậc nhất luôn đơn điệu trên từng khoảng xác định của nó.
Lời giải chi tiết:
Ta có \(y=\frac{x+{{m}^{2}}}{x+1}\Rightarrow {y}’=\frac{1-{{m}^{2}}}{{{\left( x+1 \right)}^{2}}};\,\,\forall x\ne -\,1.\)
Hàm số đồng biến trên từng khoảng xác định \(\Leftrightarrow \,\,{y}’>0;\,\,\forall x\ne -\,1\Leftrightarrow \,\,1-{{m}^{2}}>0\Leftrightarrow \,\,m\in \left( -\,1;1 \right).\)
Chọn C.
Đáp án – Lời giải
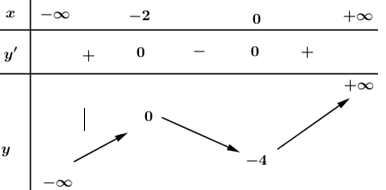
Câu hỏi 24 :
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên:
Số khoảng đồng biến của hàm số \(y=f\left( x \right)\) là:
-
A
4
-
B
2
-
C
1
-
D
3
Đáp án: B
Phương pháp giải:
Hàm số \(y=f\left( x \right)\) đồng biến (nghịch biến) trên \(\left( a;b \right)\Leftrightarrow f’\left( x \right)\ge 0\,\,\left( f’\left( x \right)\le 0 \right)\,\,\forall x\in \left( a;b \right)\) và \(f’\left( x \right)=0\) tại hữu hạn điểm.
Lời giải chi tiết:
Dựa vào BBT ta dễ thấy hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( -\infty ;-2 \right)\) và \(\left( 0;2 \right)\).
Chọn B.
Đáp án – Lời giải
Câu hỏi 25 :
Hàm số \(y=f\left( x \right)\) có đạo hàm \(y’={{x}^{2}}\). Mệnh đề nào dưới đây đúng?
-
A
Hàm số đồng biến trên \(\left( -\infty ;0 \right)\) và nghịch biến trên \(\left( 0;+\infty \right)\).
-
B
Hàm số đồng biến trên R.
-
C
Hàm số nghịch biến trên R.
-
D
Hàm số nghịch biến trên \(\left( -\infty ;0 \right)\) và đồng biến trên \(\left( 0;+\infty \right)\).
Đáp án: B
Phương pháp giải:
Hàm số \(y=f\left( x \right)\) đồng biến (nghịch biến) trên \(\left( a;b \right)\) khi và chỉ khi \(f’\left( x \right)\ge 0\,\,\left( f’\left( x \right)\le 0 \right)\,\,\forall x\in \left( a;b \right)\) và \(f’\left( x \right)=0\) tại hữu hạn điểm.
Lời giải chi tiết:
\(y’={{x}^{2}}\ge 0\,\,\forall x\in R\) và \(y’=0\Leftrightarrow x=0\). Vậy hàm số đã cho đồng biến trên R.
Chọn B.
Đáp án – Lời giải
Câu hỏi 26 :
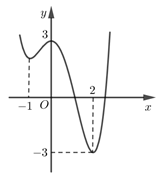
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng về hàm số đó?
-
A
Nghịch biến trên khoảng \((-3;\,\,0).\)
-
B
Đồng biến trên khoảng \((0;\,\,2).\)
-
C
Đồng biến trên khoảng \((-1;\,\,0).\)
-
D
Nghịch biến trên khoảng \((0;\,\,3).\)
Đáp án: C
Phương pháp giải:
+) Dựa vào đồ thị hàm số nhận xét những đặc điểm của đồ thì và chọn kết luận đúng.
Lời giải chi tiết:
Dựa vào đồ thị hàm số suy ra đồ thị hàm số đồng biến trên \(\left( -1;0 \right)\) và \(\left( 2;+\infty \right),\) nghịch biến trên \(\left( -\infty ;\ -1 \right)\) và \(\left( 0;2 \right).\)
Chọn C.
Đáp án – Lời giải
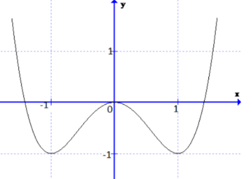
Câu hỏi 27 :
Đường cong trong hình vẽ bên là đồ thị của hàm số có dạng \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\,\,\left( a\ne 0 \right).\) Hàm số đồng biến trên khoảng nào dưới đây ?
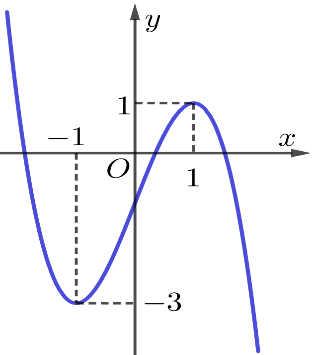
-
A
\(\left( 1;+\,\infty \right).\)
-
B
\(\left( -\,1;+\,\infty \right).\)
-
C
\(\left( -\,\infty ;1 \right).\)
-
D
\(\left( -\,1;1 \right).\)
Đáp án: D
Phương pháp giải:
Dựa vào đồ thị hàm số xác định khoảng đi lên, đi xuống để xét tính đồng biến
Lời giải chi tiết:
Dựa vào đồ thị hàm số, ta thấy hàm số đồng biến trên khoảng \(\left( -\,1;1 \right).\)
Chọn D
Đáp án – Lời giải
Câu hỏi 28 :
Cho hàm số \(y=f\left( x \right)\) thỏa mãn \({f}’\left( x \right)={{x}^{2}}-5x+4.\) Khẳng định nào sau đây là đúng ?
-
A
Hàm số đã cho đồng biến trên khoảng \(\left( -\,\infty ;3 \right).\)
-
B
Hàm số đã cho nghịch biến trên khoảng \(\left( 3;+\,\infty \right).\)
-
C
Hàm số đã cho nghịch biến trên khoảng \(\left( 2;3 \right).\)
-
D
Hàm số đã cho đồng biến trên khoảng \(\left( 1;4 \right).\)
Đáp án: C
Phương pháp giải:
Lập bảng xét dấu y’ để tìm khoảng đơn điệu của hàm số
Lời giải chi tiết:
Ta có \({f}’\left( x \right)={{x}^{2}}-5x+4=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=4 \\\end{align} \right.\) suy ra \(\left[ \begin{array}{l}x \in \left( {1;4} \right) \Rightarrow f’\left( x \right) < 0\\x \in \left( { – \infty ;1} \right) \cup \left( {4; + \infty } \right) \Rightarrow f’\left( x \right) > 0\end{array} \right.\)
Do đó, hàm số nghịch biến trên khoảng \(\left( 1;4 \right)\) và đồng biến trên khoảng \(\left( -\,\infty ;1 \right)\) và \(\left( 4;+\,\infty \right).\)
Vì \(\left( 2;3 \right)\subset \left( 1;4 \right)\) suy ra hàm số đã cho nghịch biến trên khoảng \(\left( 2;3 \right).\)
Chọn C
Đáp án – Lời giải
Câu hỏi 29 :
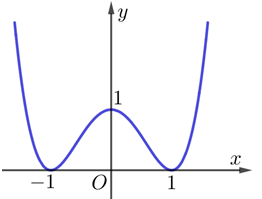
Cho hàm số \(f\left( x \right)\) liên trục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Hàm số \(f\left( x \right)\) đồng biến trên khoảng nào ?
-
A
\(\left( -\,\infty ;0 \right).\)
-
B
\(\left( -\,\infty ;-\,1 \right).\)
-
C
\(\left( 1;+\,\infty \right).\)
-
D
\(\left( -\,1;1 \right).\)
Đáp án: C
Phương pháp giải:
Dựa vào hình dáng của đồ thị để xét tính đơn điệu.
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy hàm số đồng biến trên khoảng \(\left( -\,1;0 \right)\) và \(\left( 1;+\,\infty \right).\)
Chọn C
Đáp án – Lời giải
Câu hỏi 30 :
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
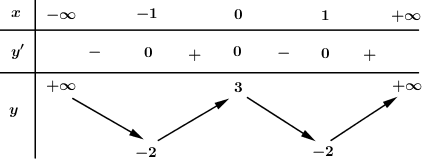
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A
\(\left( { – 2; + \infty } \right)\)
-
B
\(\left( {1; + \infty } \right)\)
-
C
\(\left( { – 2;3} \right)\)
-
D
\(\left( { – \infty ; – 1} \right)\)
Đáp án: B
Phương pháp giải:
Dựa vào bảng biến thiên để xác định tính đồng biến của hàm số ứng với khoảng mà hàm số liên tục và có đạo hàm dương.
Lời giải chi tiết:
Dựa vào bảng biến thiên ta có hàm số đồng biến trên các khoảng \(\left( { – 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Chọn B.
Đáp án – Lời giải















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


