Electric Power and Efficiency of Electric Device

Mục Lục

Power or Electric Power

The rate at which work is done in an electric circuit is called as electric power. In other word, the work done per unit time is termed as electric power. It is denoted p or P.

Formula and Unit of Power

When voltage is applied across a resistor, it causes current to flow through it. Therefore, work is being done in moving the electrons through the resistor in a unit time is called the electric power.

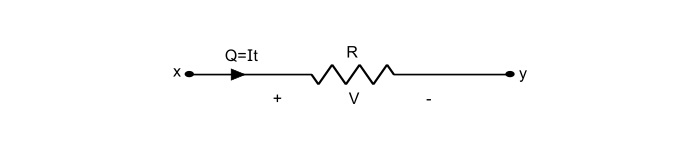
Referring the above figure,

$$\mathrm{V=\frac{work}{Q}}$$

$$\mathrm{\Rightarrow work(W)=VQ=VIt}$$

As, the power is defined as work done per unit time i.e.

$$\mathrm{Power(P)=\frac{work\:done\:in\:electric\:circuit(W)}{Time(t)}=\frac{VIt}{t}}$$

$$\mathrm{(∵V=IR\:or\:I=\frac{V}{R})}$$

$$\mathrm{∴P=VI=I^2R=\frac{V^2}{R}}$$

The above three formulae are equally valid for power calculation. Which one is used depends on the known quantities.

Since, the work done is measure in joules and time in seconds. Therefore, the unit of power is joule/sec or watt i.e.

$$\mathrm{Unit\:of\:Power=\frac{joule}{seconds}=watt}$$

Hence, the power consumed in an electric circuit is 1 watt, if a potential difference of 1 V causes 1 A current to flow through the circuit.

The larger units of power are Kilowatts (kW) Megawatts (MW), and Gigawatts (GW).

$$\mathrm{1\:kW=1000\:W;1MW=10^6\:W=10^3\:kW;1\:GW=10^9W}$$

Sometimes, power is also measured in Horse Power (h.p.),

1 horse power (h.p.) = 746 Watts

Expressions of the power

Expressions of power in the translational system,

$$\mathrm{Power=\frac{Work\:Done}{Time}=\frac{Force×Distance}{Time}=Force×Velocity}$$

Expression of power in the rotational system, If a body makes N r.p.m. and the torque acting on it is τ Newton-meter, then,

$$\mathrm{Work\:done/minute = 2\pi Nτ\:joules}$$

$$\mathrm{Work\:done/sec =\frac{2\pi Nτ}{60}joules/sec}$$

Therefore,

$$\mathrm{Power(P)=\frac{2\pi Nτ}{60}joules/sec\:or\:watts}$$

$$\mathrm{(∵\:746\:watts = 1 h. p. )}$$

$$\mathrm{∴\:Power\:(P)=\frac{2\pi Nτ}{60×746}h.p}$$

Efficiency of Electric Device

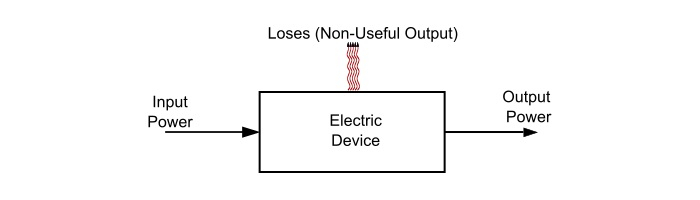
The efficiency of an electric device is defined as the ratio of useful output power to the
input power, i.e.,

$$\mathrm{Efficiency(\eta)=\frac{Useful\:Output\:Power(P_{o})}{Input\:Power(P_{i})}}$$

As, the efficiency is the ratio of output and input powers, thus it is a dimensionless quantity.
Generally, the efficiency of a device is measured in percentage (%), as,

$$\mathrm{\%\:Efficiency(\eta)=\frac{Useful\:Output\:Power(P_{o})}{Input\:Power(P_{i})} × 100 \%}$$

Some electrical devices have efficiency nearly equal to 100%. An example of such device is electric heater, in which all the input electrical energy is converted into heat energy.

Harmful Effects of Poor Efficiency

The harmful effects of poor efficiency are as follows −

Poor efficiency of the device means greater the losses, thus a large amount of energy
is wasted on non-useful output.
The non-useful output appears in the form of heat that raises the temperature of the
device. Therefore, poor efficiency means a significant temperature rise. The devices
that run hot are more likely to fail.
The heat produced due to poor efficiency has to be dissipated. Thus, the heat
removal system increases the cost and size of the device.

Numerical Example – 1

An electric motor is developing a torque of 60 N-m at a speed of 1500 r.p.m. Calculate the
power developed by the motor in Watt and h.p.

Solution

$$\mathrm{Power\:developed\:by\:motor,P=\frac{2\pi Nτ}{60}=\frac{2\pi×1500×60}{60}=9420 W}$$

$$\mathrm{(∵\:746\:Watts = 1 h. p. )}$$

$$\mathrm{∴p=\frac{Power\:in\:watts}{746}=\frac{9420}{746}=12.63 h. p.}$$

Numerical Example – 2

A lift of 200 kg mass is raised with a velocity of 10 m/s. if the input power to the driving
motor is 21.42 kW. Calculate the % efficiency of the motor.

Solution

Weight of the lift,F = mg = 200 × 9.81 = 1962 Newton

Output power of the motor = Force × Velocity = 1962 × 10 = 19620 W = 19.62 kW

$$\mathrm{\%\:Efficiency=\frac{Output\:power\:of\:motor}{Input\:power\:of\:motor}× 100\:\%\:=\frac{19.62}{21.42}× 100 = 91.59\%}$$