Bài 110 : Thể tích của một hình – VBT Toán – Tìm đáp án, giải bài tập,
Bài 1
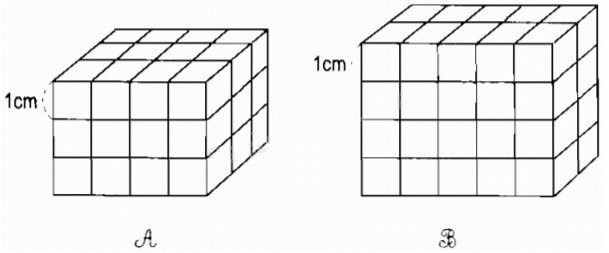
Cho hai hình A và B như hình dưới đây :
Hình A gồm bao nhiêu hình lập phương nhỏ ?
Hình B gồm bao nhiêu hình lập phương nhỏ ?
Hình nào có thể tích lớn hơn ?
Phương pháp giải:
Quan sát hình vẽ để tính số hình lập phương nhỏ của mỗi hình. Hình nào có nhiều hình lập phương nhỏ hơn thì có thể tích lớn hơn.
Lời giải chi tiết:
Số hình lập phương nhỏ ở hình A là :
4 × 3 × 3 = 36 (hình)
Số hình lập phương nhỏ ở hình B là :
5 × 4 × 2 = 40 (hình)
Hình A gồm 36 hình lập phương nhỏ.
Hình B gồm 40 hình lập phương nhỏ.
Hình B có thể tích lớn hơn hình A.
Bài 2
Viết tiếp vào chỗ trống cho thích hợp :
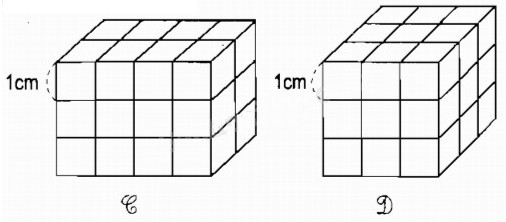
a) Hình hộp chữ nhật C gồm ……… hình lập phương nhỏ.
b) Hình lập phương D gồm ………… hình lập phương nhỏ.
c) Thể tích hình lập phương D ……… thể tích hình hộp chữ nhật C.
Phương pháp giải:
Quan sát hình vẽ để tính số hình lập phương nhỏ của mỗi hình. Hình nào có nhiều hình lập phương nhỏ hơn thì có thể tích lớn hơn.
Lời giải chi tiết:
a) Hình hộp chữ nhật C gồm 4 × 2 × 3 = 24 hình lập phương nhỏ.
b) Hình lập phương D gồm 3 × 3 × 3 = 27 hình lập phương nhỏ.
c) Thể tích hình lập phương D lớn hơn thể tích hình hộp chữ nhật C.
Bài 3
Một hình lập phương được tạo bởi 8 khối gỗ hình lập phương cạnh 1cm và một hình lập phương khác được tạo bởi 27 khối gỗ hình lập phương cạnh 1cm. Hỏi có thể xếp tất cả các khối gỗ của hai hình lập phương trên thành một hình lập phương mới không ?
Phương pháp giải:
Tìm tổng số khối gỗ của hai hình lập phương, ta giả sử là N. Nếu có số tự nhiên a sao cho a × a × a = N thì ta có thể xếp được hình lập phương mới có độ dài cạnh là a.
Lời giải chi tiết:
Ta có : \(8 = 2 × 2 × 2\) ; \(27 = 3 × 3 × 3\)
Tổng các khối gỗ của hai hình lập phương là:
\(8 + 27 = 35\) (khối)
Không có số tự nhiên \(a\) nào để: \(a × a × a = 35\).
Do đó không thể xêp được tất cả các khối gỗ của hai hình lập phương đã cho thành một hình lập phương mới.















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


